第73問の解答
問題 [場合の数]
|
|
|
|
|
|
ある整数をいくつかの整数の和で表すことを考えます。 例えば、3ならば、1+1+1=3、1+2=3、2+1=3の3通りが考えられますね。 また、4ならば、1+1+1+1=4、1+1+2=4、1+2+1=4、2+1+1=4、1+3=4、3+1=4、2+2=4の7通りが考えられます。 では、同様の方法で、10をいくつかの整数の和で表すとき、全部で何通りの表し方があるでしょうか。 |
|
|
|
|
|
解答例1
マサルさん
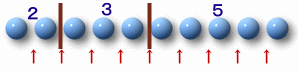
10個のボールを並べて、ボールとボールの間に仕切りを入れることを考えます。
例えば、2番目と3番目の間、5番目と6番目の間に仕切りを入れると、
となり、これは 2+5+3=10 を表していると考えることができます。
従って、この問題ではこの仕切りの入れ方が何通りあるかを考えればよいわけです。
すると、仕切りを入れることの出来る場所は10−1=9箇所あります。
この9箇所それぞれに、仕切りを入れる場合と入れない場合の2通りずつありますから、
仕切りの入れ方は全部で、29=512通りあることになります。しかしこれだと、全く仕切りを入れない場合、つまり10=10の場合が含まれているので、
その分だけ除きます。従って、全部で512−1=511通りあることが分かります。
答: 511通り
以上