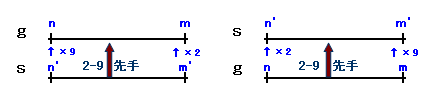第76問の解答
問題 [推理]
|
|
|
|
|
|
リエさんとキョーコさんが、2〜9の整数を使って次のようなゲームをしました。
このようにして、ゲームを続けていき、2000以上の数を作った方が勝ちとします。 さて、リエさんがはじめに2と言ったそうです。 では、キョーコさんが言った絶対に勝てる数とは何だったと考えられるでしょうか。 |
|
|
|
|
|
解答例1
マサルさん
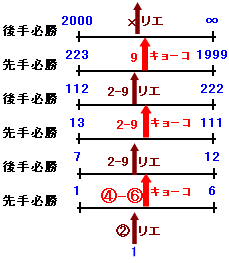
下図のように考えます。ここで先手勝とは、先手番がうまくやれば必勝となる状態、
また、後手勝とは、先手番がどのような手をつくしても後手が必勝となる状態 を表します。
キョーコさんが必ず勝つわけですから、その直前にリエさんが作った数は、2000より小さい数で、223以上(9倍すると2000を越える)の数のはずです。というよりも、リエさんをそのような数を作らざるを得ない状況に追い込めばよいわけです。
そのためにはその前のキョーコさんの数は、112以上で222以下の数であればよいことになりますね。こうなると、リエさんは2と言っても224、9と言っても1998となり、どうしても上記の範囲の数を作ってしまうことになります。
また、キョーコさんが112より大きく222以下の数を作るには、そのまた前にリエさんが作った数が13以上で111以下の数であればよいことになります。つまり、キョーコさんはこの状況に追い込んだわけです。
さて、リエさんがどうしても13以上で111以下の数になるということは、キョーコさんがその前に作った数が7以上で12以下であることになりますね。(13以上だと9を掛けると111を越えてしまいます。)
キョーコさんが7以上で12以下の数を作るわけですから、リエさんの言った数が2であることを考えると、
2×4=8
2×5=10
2×6=12
の3通りが、必ず勝てる方法ということになりますね。
答: 4、5、6
以上
(参考)式で考えてみます。
後手必勝形の区間をg(n,m)、先手必勝形の区間をs(n',m')と書くことにします。
まず、g(2000,∞)ですね。
先手必勝形から後手必勝形になるには、
m'+1≦n≦n'×9、m'×2≦m
であればいいので、
n'=[n/9]↑、m'=[m/2]↓またはn-1
となります。(ただし、[ ]↑は切上げ、[ ]↓は切下げを表します。)また後手必勝形から先手必勝形になるには、
m+1≦n' 、n×2≦n'、m×2≦m'
であればいいので、
n=[n'/2]↑、m=[m'/9]↓またはn'-1
となります。(ただし、[ ]↑は切上げ、[ ]↓は切下げを表します。)従って、s(n',m')→g(2000,∞)となるには、
n'=[2000/9]↑=[222.22]↑=223、m'=2000-1=1999g(n,m)→s(223,1999)となるには、
n=[223/2]↑=[111.5]↑=112、m=[1999/9]↓=[222.11]=222s(n',m')→g(112,222)となるには、
n'=[112/9]↑=[12.44]↑=13、m'=[222/2]↓=111g(n,m)→s(13,111)となるには、
n=[13/2]↑=[6.5]↑=7、m=[111/9]↓=[12.33]↓=12s(n',m')→g(7,12)となるには、
n'=[7/9]↑=[0.77]↑=1、m'=[12/2]↓=6従って、最初にリエさんは、7〜9の整数を言えば、次の後手番に後手必勝形に持ち込めたことになります。
ところが、リエさんは2を言ったのでこの時点で先手必勝形になってしまったわけです。
キョーコさんがここで整数xを言って、g(7,12)に持ち込むには、
7≦2x≦12となればいいので、x=4、5、6となります。