第７７問の解答

問題　［空間図形］

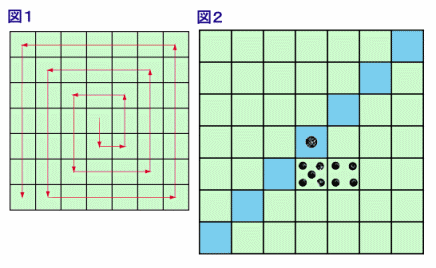問題図 各面に黒いインクをつけたサイコロと、一つのマスの大きさがサイコロの面の大きさと等しい、縦横７マスずつの方眼紙を用意し、中央にサイコロを置きました。

このサイコロを、図１の矢印のように転がしていきます。すると、２回転したところで図２のようにインクが方眼紙につきました。

では、予定通りにサイコロを転がし終わった後、図２の水色の部分（真ん中は１ですね）についたサイコロの目の和はいくつでしょうか。

解答例１

マサルさん

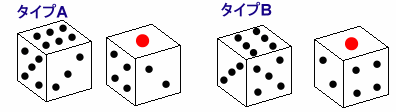
サイコロの目の配置には、次の２通りのパターンがあるようです。
問題のような結果となるのは、タイプBのほうになります。

参考図１

さて、この問題では、サイコロを転がすことに関して、２つの重要な性質を利用します。
その性質とは、

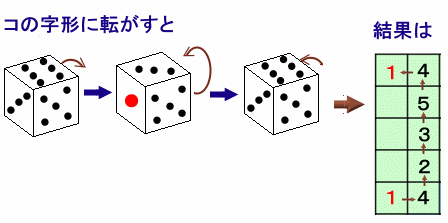
  1. 同じ方向に２回転がすと対面が下にくる。さらに２回転すると元に戻る。

従って、サイコロの目は対面の合計が７になっているので、
例えば、今下に４がきているとすると、同じ方向に２回転がすと下には３がきて、さらに２回転すると４に戻るというわけです。

  1. コの字型に転がしたとき
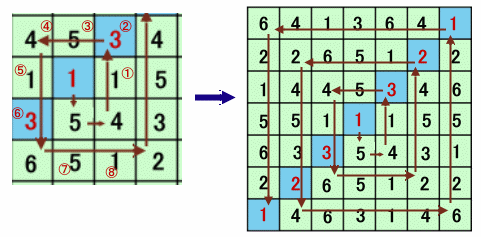
    下図の例で、赤い数字１に注目してみて下さい。

参考図２

さて、この２つの性質を利用して数字を埋めていきます。

参考図３

  1. コの字型の性質より、左側のマスと同じ１

  2. ２回転したので、２つ下の４と対角の３

  3. コの字型の性質より、２つ下のマスと同じ５

  4. ２回転下ので、２つ右の３と対角の４

  5. コの字型の性質より、２つ右のマスと同じ１

  6. ２回転したので、２つ上の４と対角の３、および１と対角の６

  7. コの字型の性質より、３つ上のマスと同じ５

  8. ２回転したので、２つ左の６と対角の１、および５と対角の２
    ・・・・

というわけで、結果は上の右図のようになります。

従って、対角線上に並ぶ数字の和は＝１＋２＋３＋１＋３＋２＋１＝１３　となります。

答：　１３

以上