第79問の解答
問題 [規則性]
|
|
|
|
|
|
|
 |
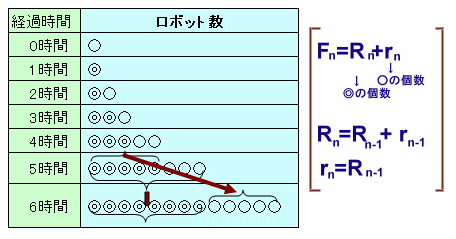
マサル研究所では、自己増殖型ロボットの研究をしています。 このロボットは、自分と同じタイプのロボットを1時間に1個作ることができます。また、作られたばかりのロボットは始めの1時間は動作テストのためにロボットの生産をしませんが、その後はやはり同じように1時間に1個のロボットを作ります。 いま、作られたばかりのロボットを1個用意しました。そして、1時間ごとにロボットの個数を調べたところ、左図のようになっていました。 さて、このようにして1時間ごとに500時間後までを調査するとき、ロボットの個数が3の倍数になっていることは何回あるでしょうか。 |
|
|
|
|
|
|
解答例1
マサルさん
算チャレでもおなじみのフィボナッチ数列に関する問題です。
フィボナッチ数列(一般項をFnとします)は、Fn=Fn-1+Fn-2となるような数列で、例えば、
1、2、3、5、8、13、21、34、55、・・・
のように、本問のロボット個数もフィボナッチ数列になります。なぜなら、作られたばかりのロボットは働くことはできませんね。
この子供ロボットを○とし、n時間後の個数をrnとします。また、1時間経過したロボットは働く(生産する)ことができます。
この大人ロボットを◎とし、n時間後の個数をRnとします。大人、子供合わせたロボット数をFnとして、時間ごとの様子を以下の表に表してみます。
すると、
Fn=Rn+rn ・・・ (1)
Rn=Rn-1+rn-1 ・・・ (2)
rn=Rn-1 ・・・ (3)
が成り立ちます。(2)、(3)より、
Rn=Rn-1+rn-1=Rn-1+Rn-2 ・・・ (4)また、(3)、(4)より、
rn=Rn-1=Rn-2+Rn-3=rn-1+rn-2 ・・・ (5)(1)、(4)、(5)より、
Fn=Rn+rn=(Rn-1+Rn-2)+(rn-1+rn-2)
=(Rn-1+rn-1)+(Rn-2+rn-2)
=Fn-1+Fn-2 ・・・ (6)(6)より、ロボット数がフィボナッチ数列の性質を持っていることが分かりました。
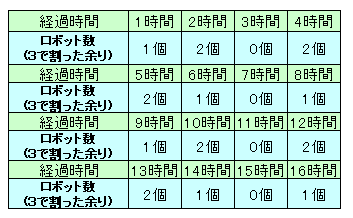
あとは3の倍数がどの頻度で表れるかを調べるだけです。
実は、結論から言うと3の倍数は4回に1回現れます。これは少し調べてみれば分かります。
これは、3で割った余りを考えると分かりやすいはずです。
式で考えると、(6)より、
Fn+1=Fn+Fn-1=(Fn+Fn-1)+Fn-1=Fn+2Fn-1
Fn+2=Fn+1+Fn=(Fn+2Fn-1)+(Fn+Fn-1)=2Fn+3Fn-1
Fn+3=Fn+2+Fn+1=(2Fn+3Fn-1)+(Fn+2Fn-1)=3Fn+5Fn-1
よって、
Fn+4=3Fn+1+5Fn=3(Fn+1+Fn)+2Fn・・・ (7)(7)より、Fnが3の倍数だと、Fn+4も3の倍数となります。
逆に、Fnが3の倍数でないと(3で割った余りが1または2)、2Fnを3で割った余りは2または1となって、3の倍数でありません。上図より、1〜4時間後では、3時間後のみ余りが0なので、その後も4時間ごとに余りが0(3の倍数)が現れることになります。
従って、1〜500時間後までだと、3の倍数は、
500÷4=125回となることが分かります。答: 125回
以上