第81問の解答
問題 [空間図形]
|
|
|
|
|
|
|
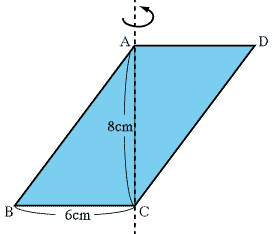 |
左図のような、BC=6cm、AC=8cmの平行四辺形ABCDがあります。 この平行四辺形をACを軸にして270度回転させたときにできる立体の体積を求めて下さい。(ただし、円周率は3とします。) |
|
|
|
|
|
|
解答例1
マサルさん
まずは完成した立体が上下対称であることに注目します。
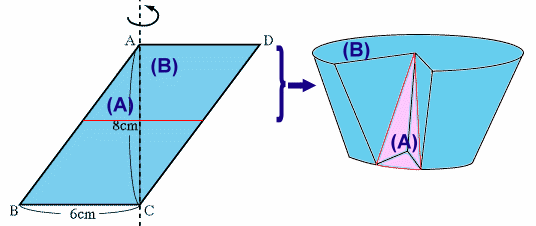
従って、上半分か下半分の立体の体積を求めて、それを2倍すればよい、ということになるわけです。そこで、下の図のようにもとの平行四辺形を上下に2分割し、上半分を270゜回転させると下の右図のようになります。
この立体は、半径6cm、高さ8cmの円錐(以下、単に円錐といいます)から切りとられた2つの部品で構成されています。
1つは上の図の赤い部分(A)です。
これは、円錐をちょうど半分の高さで、底面と平行な平面で切ったときの上半分の4分の1になっています。(中心角が90゜ )従って、(A)の体積は、
(底面の面積)×(高さ)÷3×(上の部分)×(中心角90゜)÷360°
=6×6×3×8÷3×1/8×1/4=9cm3
もう一つは上の図のその他の部分(B)です。
これは、円錐をちょうど半分の高さで、底面と平行な平面で切ったときの下半分の4分の3になっています。(中心角は270゜)従って、(B)の体積は、
(底面の面積)×(高さ)÷3×(下の部分)×(中心角270゜)÷360°
=6×6×3×8÷3×7/8×3/4=189cm3
求める体積は、この合計しの2倍だから、
(189+9)×2=396cm3となります。答: 396cm3
以上