第85問の解答
問題 [平面図形]
|
|
|
|
|
|
|
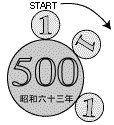 |
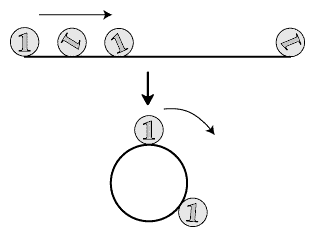
左図のSTART地点から、1円玉が500円玉の周りをすべることなく転がっていきます。 では、1円玉の位置・向きともに再び図のSTART地点の状態になるまでに、1という数字は何回転するでしょうか。 ただし、500円玉の直径は2.7cm、1円玉の直径は1cmとします。 (注)ここでの1回転は、1という数字が上を向いた状態から一旦下を向き、再び上を向くまでを指します。 |
|
|
|
|
|
|
解答例1
マサルさん
まず、500円玉の外周と同じ長さの直線上を1円玉が転がる場合を考えます。
500円玉の外周は2.7cm×円周率で、1円玉の外周は1×円周率です。
従って、(2.7×円周率)÷(1×円周率)=2.7回転 するはずです。
ところが、この直線をまるめて円にすると、1円玉が1周余計に回っていることが分かります。
従って、1円玉が500円玉の回りを1周するとき、1円玉自信は2.7+1=3.7回転することになります。
また、1円玉は向き・位置ともに同じにならなくてはなりません。
1円玉が500円玉の回りを1周した状態では、1円玉は3.7回転ですから、向きが違いますね。この回転数が整数になれば、位置も向きも同じということになります。
3.7回転を10回繰り返せば37回転と、はじめて整数なるので、問題の答えは37回転ということになります。
答: 37回転
以上