第87問の解答
問題 [空間図形]
|
|
|
|
|
|
|
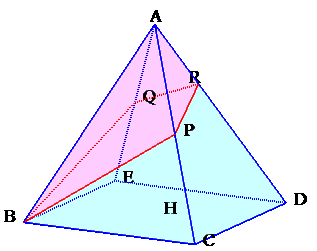 |
左図は、正四角錐A−BCDEを、B、P、Qを通る平面で切ったものです。 P、QがそれぞれAC、AEの中点であるとき、Aを含む方の立体の体積は正四角錐の何倍でしょうか。 |
|
|
|
|
|
|
解答例1
マサルさん
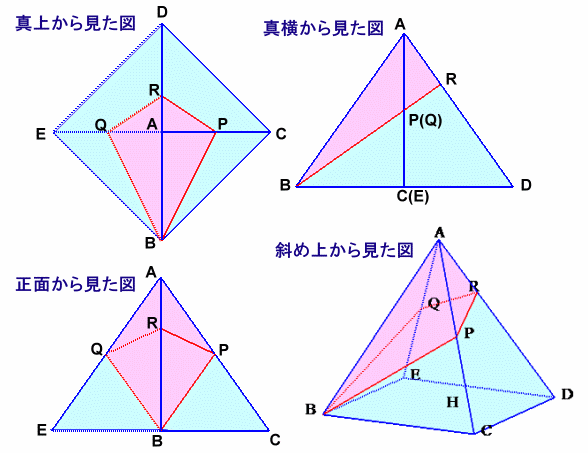
問題の立体を各方向から見ると下記のようになっています。
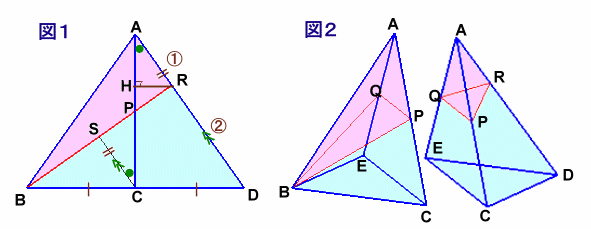
そこで、平面ABDで切った断面をCのほうから見たものを図1、
また、平面ACEで立体を2分割したものを図2とします。
Cを通りDAに平行に引いた直線とBRの交点をS、およびRからACに下ろした垂線の足をHとします。
△SBCと△RBDは相似で、相似比はBC:BD=1:2、
よって、CS:DR=1:2。 ・・・ (1)また、△APRと△CPSは相似で、かつAP=CPより、2つの三角形は合同。
よって、AR=CS。 ・・・ (2)(1)、(2)より、AR:RD=1:2。
さらに、△ARHと△ADCは相似で、相似比はAR:AD=1:3。
よって、RH:DC=1:3。 ・・・ (3)正四角錐A−BCDEの体積をVとします。
図2で、三角錐B−APQとB−ACEの比を求めましょう。
底面の比は△APQ:△ACE=1:4、
高さは共通、よって体積比は1:4。三角錐B−APQ=三角錐B−ACE×1/4=V×1/2×1/4=V×1/8 ・・・ (4)
また、三角錐R−APQとD−ACEの比を求めましょう。
底面の比は△APQ:△ACE=1:4、(なぜなら、AP=AC×1/2、AQ=AE×1/2)
高さの比はRH:DC=1:3、よって体積比は1:12。三角錐R−APQ=三角錐D−ACE×1/4=V×1/2×1/12=V×1/24 ・・・ (5)
従って、四角錐A−BPQR
=角錐B−APQ+三角錐R−APQ
=V×1/8+V×1/24
=V×1/24×(3+1)
=V×1/6答: 1/6
以上