第８８問の解答

問題　［ 平面図形］

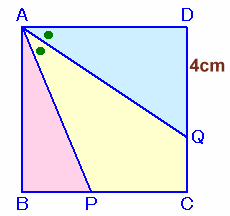問題図 左図の四角形ＡＢＣＤは正方形です。

点ＰはＢＣ上の点で、∠ＰＡＱ＝∠ＱＡＤとなっています。
また、各部の面積比は以下の通りです。

△ＡＢＰ：四角形ＡＰＣＱ：△ＡＱＤ＝５：１１：８

では、ＱＤ＝４cmであるとき、ＡＰの長さは何cmでしょうか。

解答例１

ヨッシーさん

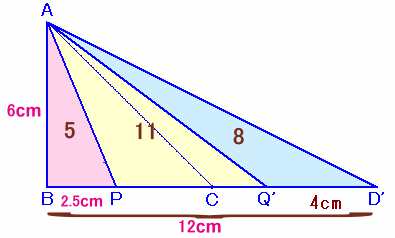
BCの延長線上にQ'およびD'をCQ'＝CQ、Q'D'＝QD＝4cmとなるようにとります。

参考図１

△ACQ'＝1/2×CQ'×AB＝1/2×CQ×AD＝△ACQ、
△AQ'D'＝1/2×Q'D'×AB＝1/2×Q'D'×AD＝△AQD。

よって、△ABP：△APQ'：△AQ'D'＝５：１１：８。
従って、BP：PQ'：Q'D'＝５：１１：８。

よって、BP＝Q'D'×5/8＝４×5/8＝２.５cm、　・・・　（１）
また、BD'＝Q'D'×（5+11+8）/8＝４×24/8＝１２cm。

BD'＝BC×２より、AB＝BC＝１２×1/2＝６cm。　・・・　（２）

（１）、（２）より、△ABPは辺の長さが５：１２：１３の直角三角形と分かります。

よって、AP＝１３×2.5/５＝６.５cm　となります。

答：　６.５cm

以上