第89問の解答
問題 [推理]
|
|
|
|
|
|
ある中学校には、全部で351人の生徒がいます。 この学校で友達の人数をアンケート調査してみたところ、意外なことに?最も多い人でも6人でした。 あるとき、この中学校の生徒を班分けすることになりました。 では、この「お互いに誰も友達でない」班は、最も少ない場合で何人であったと考えられるでしょうか。 |
|
|
|
|
|
解答例1
ヨッシーさん
「班の人数ができるだけ多くなるように」作り、それが「最も少ない場合」ですから、6人の友人を持っている人が沢山いる場合を考えればよいことになります。
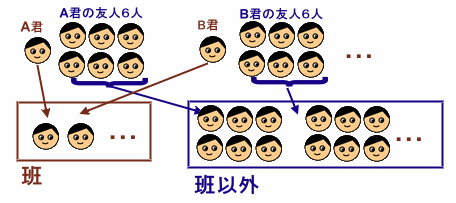
そこで、6人の友人を持っている人(A君)が、その班に入ったとします。
すると、その人の友人6人は班に入る資格を失うことになります。逆に、残った351-1-6=344人は、その班に入る資格があります。(班の1人と友人ではないですから...)
そこで、適当な人(B君)がその班に入ったとします。するとまた、6人の人が資格を失います。
このように考えると、1人が班に入るたびに残りの人数から6人が資格を失っていくことになります。つまり、1度に7人ずつ消えていくことになります。
従って、351人が7人ごとのグループがいくつできるかを計算すればいいことになります。 351÷7=50 余り 1 ですから、切り上げて51グループできます。
よって、この班には51人いることになります。
答: 51人
以上