第91問の解答
問題 [平面図形]
|
|
|
|
|
|
|
 |
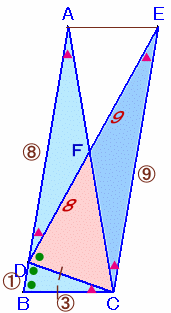
AB:BC=3:1である二等辺三角形ABCがあります。 左図は、この△ABCを頂点Cを中心に回転し、頂点Bが辺AB上にきたところを表しています。 このとき、図の△FDCの面積は、もとの△ABCの何倍でしょうか。 |
|
|
|
|
|
|
解答例1
ヨッシーさん
△ABCと△EDCは合同な二等辺三角形になります。
従って、CD=CBとなり、△CDBも二等辺三角形。
また、∠CBD=∠ABCより、△CDBは△ABCと相似。よって、∠DCB=∠BAC。
すると、∠FCE
=∠ECD−∠FCD
=∠ACB−∠FCD
=∠DCB=∠CFE。従って、△FCEはFE=FCの二等辺三角形。
また、∠FDA=180°−(∠EDC+∠CDB)
=180°−(∠EDC+∠ACB)
=∠DAF従って、△FADもFA=FDの二等辺三角形で、しかも△FCEと相似。
ここで、AB=EC=9とすると、
AB:BC=3:1より、BC=9×1/3=3。よって、DB=BC×1/3=3×1/3=1。
従って、AD=AB−DB=9−1=8。
これより、△FADと△FCEは相似で、相似比はCE:AD=9:8、
よって、EF:FD=9:8。従って、△FDC=△EDC×8/(8+9)=△ABC×8/17 となります。
答: 8/17倍
以上