第９２問の解答

問題　［規則性］

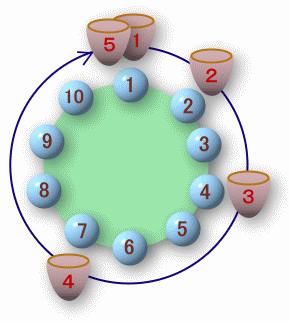問題図 左図のように丸テーブルに１番から１０番までの番号が振られています。

抽選で各テーブルに全員が着席した後、次のようなゲームが始まりました。

  1. まず１番の席の人がカゴの中に１００円を入れます。
    そしてカゴを時計周りに１つ進めます。
  2. カゴがまわってきた２番の席の人は中に１００円を入れます。
    そしてカゴを時計周りに２つ進めます。
  3. 同様にして、カゴがまわってきた人は中に１００円を入れます。
    そしてカゴを時計周りに「前回進んだ数＋１」だけ進めます。

このようにして、カゴの中に７５００円貯まったところで終了とします。

このとき、一番多い人でお金をいくら入れたでしょうか。

解答例１

ヨッシーさん

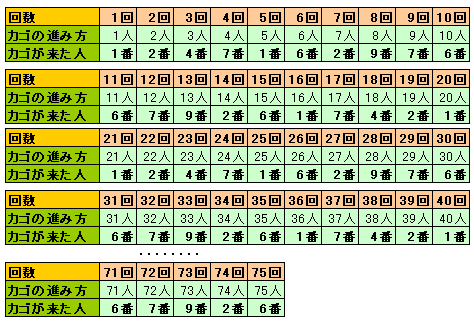
終了時点でカゴに貯まっていたのは７５００円ですから、７５００÷１００＝７５回の支払いが行われました。

参考図１

参考図２

１回目から１０回目までを調べると、カゴが回って来た人の番号は、
　　１、２、４、７、１、６、２、９、７、６　
となり、支払い回数は、
　　１が２回、２が２回、４が１回、６が２回、７が２回、９が１回
となります。

さらに２０回まで調べます。
１１，１２　と進めるのは、１，２　と進めるのと同じなので、１１回目から２０回目までは、上記の数が５ずつずれて、
　　６，７，９，２，６，１，７，４，２，１
となり、支払い回数は、
　１が２回、２が２回、４が１回、６が２回、７が２回、９が１回
と１回目から１０回目までと同じになります。

ここで１に戻ったので、このあと１０回ごとに、同じ回数ずつ増えていきます。

従って、７０回目までで、
　１が１４回、２が１４回、４が７回、６が１４回、７が１４回、９が７回
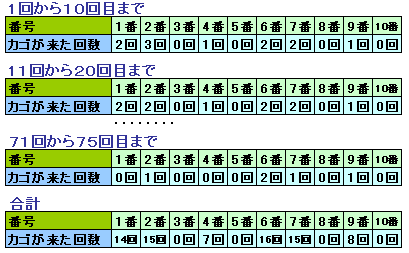
支払うことになります。

７１回から７５回までは、６、７、９、２、６
と続くので、結局６番目の人が最も多く、１６回払ったことになります。
また、支配金額は、１００円×１６回＝１６００円となります。

答：　１６００円

以上