第97問の解答
問題 [ 場合の数]
|
|
|
|
|
|
|
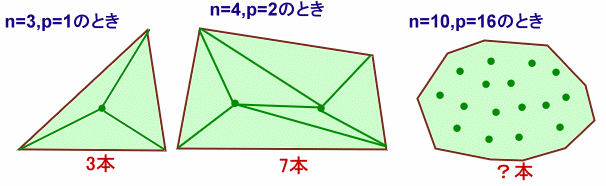 |
凸型10角形の内部に16個の点があります。 これら10角形の頂点10個+内部の点16個=26個の点を結べるだけ結びます。 このとき、線は最大何本引けるでしょうか。
|
|
|
|
|
|
|
解答例1
マサルさん
10角形の内部に点が16個ある、ということで、線を結べるだけ結んでいくと、この10角形の内部にはいくつかの三角形ができ ます。この三角形の個数が分かれば、線の本数も分かります。
一般化して、凸n角形の内部に点がp個ある場合を考えてみましょう。
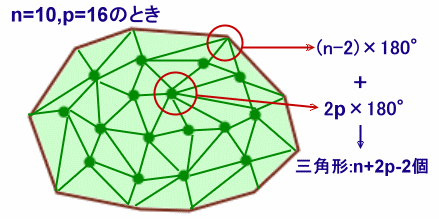
さて三角形の個数を特定するのに有効な方法は、角度を考えることです。
n角形の内部にできる三角形の角度の総和を求めるわけです。1つの点の周りの角度は360゜で、p個の点があるわけですから、それらの点の周りにできる角度は全部でp×360°=2p×180゜。
また、n角形の内角の和は、(n-2)×180゜、
従って、両者を合計すると、(n+2p-2)×180゜となります。1つの三角形の内角の和は180゜ですから、(n+2p-2)×180゜÷180=(n+2p-2)個の三角形があることになります。
すると、辺の数は(n+2p-2)個×3=(3n+6p-6)本となりますが、
まずこれからn角形の辺の数nを除いて、(2n+6p-6)本。そして、n角形の内部にできる辺は、それぞれ2つの三角形で共有していますので、
その分を差し引くと、(2n+6p-6)÷2=(n+3p-3)本 となります。本問では、n=10、p=16なので、n+3p-3=10+3×16−3=55本 と求まります。
答: 55本
以上