第100問の解答
問題 [速さの問題]
|
|
|
|
|
|
ここは東京某駅。構内のA地点とB地点は「動く歩道」で結ばれています。 この歩道は、A→B、B→Aの両方向が設置されており、どちらも同じ速さで動いています。 もちろん、距離も同じです。 いま、マサルさんはA→B方向、トモエさんはB→A方向の「動く歩道」に同時に乗りました。 その後マサルさんはペースはそのままで歩幅を10cm増加させて進み、トモエさんは歩幅はそのままでペースを1.5倍にして進んだところ、トモエさんが72歩歩いたところでA地点に到着し、そのときマサルさんはB地点の8m手前でした。
|
|
|
|
|
|
解答例1
ヨッシーさん
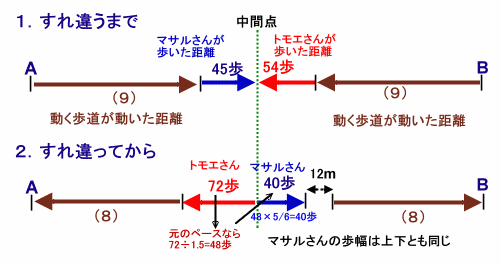
2人がすれ違うまでと、すれ違ったあとに分けて、下記のような線分図で表します。
前半部分で「マサルさんは45歩、トモエさんは54歩歩いたところですれ違った」ことから、
2人は同じ時間・同じ距離を歩いているので、
歩幅 ・・・ マサルさんの歩幅:トモエさんの歩幅=54:45=6:5
ペース ・・・ マサルさんのペース:トモエさんのペース=5:6
となります。
後半部分で、トモエさんがペースを1.5倍にして72歩歩いたときの所要時間は、
元のペースで歩いたときの、 72歩÷1.5=48歩 にかかる時間と同じです。この間に、マサルさんは 48歩×5/6=40歩 歩いています。
もし、マサルさんが、歩幅を10cm増加させずに歩いたとすると、
トモエさんがA地点に着いたとき、マサルさんは、B地点より、
8m+0.1m/歩×40歩=12m
手前にいることになります。前半と後半の時間比
=トモエさんが同じペースで歩いた場合の歩数比
=54:48
=9:8従って、これらの時間に歩道自身が動いた距離の比=9:8となります。
前半と後半でトモエさんが歩いた距離の差は、72−54=18歩分になり、
これが歩道の動いた差(1)に相当します。よって、すれ違うまでにトモエさんの歩いた距離は、
54÷18=3
より、歩道の(3)に相当します。マサルも同じ距離を歩きました。従って、AB間の距離は、
(9)+(3)+(3)+(9)=(24)
に相当することになります。一方、マサルさんについて考えると、
45歩÷3=15歩
より、15歩分が、(1)に相当します。すれ違ってからの図において、
空白の12m=マサルさんの5歩分(45-40)+(1)=(5/15)+(1)=(4/3)
に当たります。よって、
12m÷4/3=9m より、 (1)=9mとなります。従って、AB間の距離=9m×24=216m
および、トモエさんの歩幅=9m/歩÷18歩=0.5m=50cm と求まります。
答: (1)216m (2)50cm
以上