第２０１問の解答

１．問題　［規則性］

円状のコースの周りをＡさん・Ｂさん・Ｃさんが走ります。

Ａさんは４５秒、Ｂさんは９０秒、Ｃさんは３６秒でこのコースを１周することができるそうです。

３人はコースの同じ地点から同時に出発し、ＡさんとＢさんは左まわり、Ｃさんは右まわりで走ります。

コースの中心をＯとするとき、角ＣＯＢの大きさと角ＣＯＡの大きさが、９回目に等しくなるのは出発してから何秒後でしょうか。ただし、２人以上が同じ地点にいる場合は数えないものとします。

２．解答例１（香川仁志さん、航介さん、武田浩紀さん、長野美光さん、他）

Ａ、Ｂ、Ｃさんが円周を回る速度（左回りを正にとる）は、
　　Ａさん：３６０／４５＝８度/秒
　　Ｂさん：３６０／９０＝４度/秒
　　Ｃさん：３６０／３６＝−１０度/秒
となるので、Ｃさんを固定して考えると、Ａさん、Ｂさんが円周を回る相対的な速度は、
　　Ａさん：８−（−１０）＝１８度/秒
　　Ｂさん：４−（−１０）＝１４度/秒
となります。

図１
参考図1		 図２
参考図2

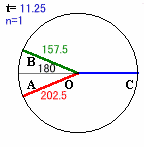
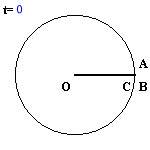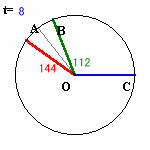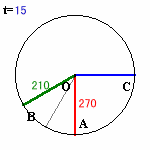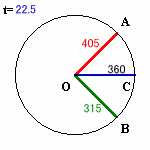
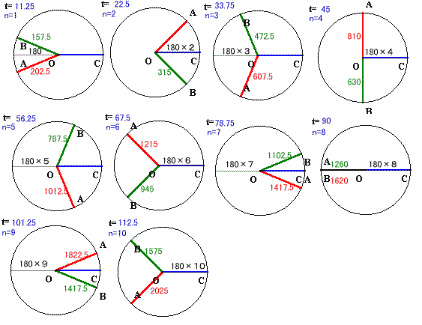
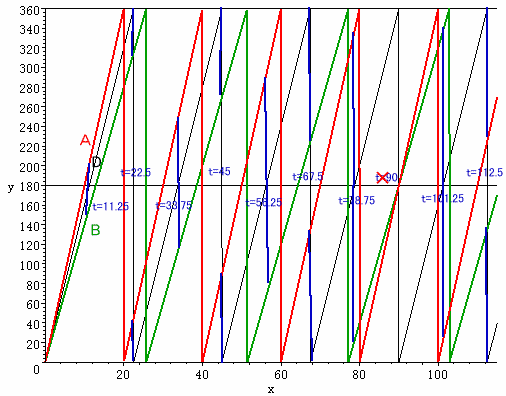
角ＣＯＢの大きさと角ＣＯＡの大きさが等しくなるのは、ＡとＢの中間点ＤがちょうどＣの反対側またはＣと重なるときとなります。

Ｄの相対速度は、（１８＋１４）／２＝１６度/秒なので、
それは１８０／１６＝１１．２５秒ごとになります。

ところが、ＤとＡ、Ｂとの角度は２度/秒、すなわちＤの１/８の速度で開いていくことになるので、８度に１回（１１．２５×８＝９０秒ごと）にＡ、Ｂは重なることになるので、この場合を除く必要があります。

参考図3

従って、角ＣＯＢの大きさと角ＣＯＡの大きさが、９回目に等しくなるのは、１１．２５×１０＝１１２．５秒後となります。

答：1１２．５秒後

　以上

３．解答例２（CRYING DOLPHINさん、小池克博さん、きょえぴさん、DrKさん、トトロ＠Ｎさん、他多数）

Ｃの位置を０度に固定して、Ａ、Ｂ、およびＤの動きをダイアグラムで表すと下図のようになる。

参考図4


ｔ＝１１．２５秒ごとに角ＣＯＢの大きさと角ＣＯＡの大きさが等しくなりますが、８回目（ｔ＝９０秒後）には、Ａ、Ｂがちょうど重なるので、これを除くと９回目に重なるのは、ｔ＝１１．２５×１０＝１１２．５秒後となります。

　以上