第２０２問の解答

---

１．問題　［比例算］

太さの異なるＡ、Ｂ、Ｃの３種類のロウソクがあります。ＡとＣは同じ長さですが、ＢはＡ・Ｃの２倍の長さがあります。 　いま、左からＡ、Ｂ、Ｃの順にロウソクを等間隔に並べて同時に火をつけたところ、Ｂのロウソクは８分後にちょうど半分が燃えつき、１２分後には３本のロウソクの頂点が一直線上に並びました。 　次に、太さがちょうどＣの半分で長さがＡ・Ｃと等しいロウソクＤを用意し、左からＡ、Ｂ、Ｄの順に等間隔に並べて同時に火をつけました。（Ａ、Ｂは新品のものと取り替えます） 　すると、今度は１５分後に３本のロウソクの頂点が一直線上に並んだそうです。 では、ＡおよびＣのロウソクはそれぞれ何分で燃え尽きるでしょうか。 注・・・ロウソクが短くなる速度は太さに反比例するものとします。

---

２．解答例１（うっしーさん、おりちゃん他）

ろうそくＡ、Ｃの頂点をＡ₀、Ｃ₀、Ｂの中点をＢ₀とします。
最初の１２分後の火の位置を、それぞれＡ₁、Ｂ₁、Ｃ₁、
２回目の１５分後の火の位置をＡ₂、Ｂ₂、Ｃ₂とします。

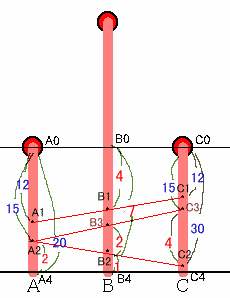
ろうそくＡでは、A₀A₁の間を燃えるのに１２分、A₀A₂の間は１５分かかるので、　A₀A₁：A₀A₂＝１２：１５

ろうそくＢでは、８分経過後のB₀B₁の間を燃えるのに４分、B₀B₂の間は７分かかるので、　B₀B₁：B₀B₂＝４：７

ろうそくＣでは、２回目の燃える速度は２倍になるので、元のＣのろうそくで考えたとき、C₀C₁の間に１２分、C₀C₂の間は３０分かかることとなり、　C₀C₁：C₀C₂＝１２：３０
となります。

今、元のろうそくＣで１５分経過したときの火の位置をＣ₃、Ａ₂とＣ₃を結ぶ直線とＢの交点をＢ₃とします。

ろうそくＡ、Ｃの長さを８とすると、
B₀B₁：B₀B₃＝１２：１５＝４：５より、B₃B₂＝２となります。

Ａ、Ｂ、Ｃは等間隔にならんでいることから、△Ｃ₃Ａ₂Ｃ₂で中点連結定理により、Ｃ₃Ｃ₂＝B₃B₂×２＝４となります。

C₀C₃：C₃C₂＝１5：３０より、C₀C₃＝C₃C₂＝４、
よってC₀C₂＝８となるので、Ｃ₂＝C₄はちょうどろうそくＣの底であり、
従ってＣは３０分で燃え尽きることになります。

また、Ｂ₂の高さは８−７＝１だから、Ａ₂はその２倍の２、
よってA₀A₂＝６、A₀A₂：A₀A₄＝６：８＝１５：２０、
従ってろうそくＡは、２０分で燃えることになります。

答：A：２０秒後、Ｂ：３０秒後

　以上

---

３．解答例２（萬田銀次郎さん、長野美光さん、Gouさん、マツダさん、パノエロさん、Hamayanさん、Taroさん、BONさん、すうぱあさん、香川仁志さん、M.Hossieさん、他多数）

A、Cの長さを１として、一分間に燃える長さの割合をそのままA、Cと 
おくと、一直線上に並んだときにＢの燃えた長さはＡ、Ｃの平均になることから、
　（１２A+１２C）／２＝４/８ 
　（１５A+３０C）／２＝８/８
これを解いて、Ａ＝１/２０、Ｃ＝１/３０を得る。 

よって、Ａ、Ｃの燃える時間は、それぞれ２０分、３０分となる。

　以上