第２０４問の解答

---

１．問題　［仕事算］

ある映画館のチケット売り場に、開店直前にずらりと行列ができていました。（注） 　売り場を２つ用意して、マサルさんとトモエさんが２人で応対したところ、６分で行列はなくなったそうです。 　翌日も同じ長さ（人数）の行列ができましたが、このときは売り場を１つにして、行列の長さが３分の１になるまではトモエさんが、その後はマサルさんが応対したところ、行列がなくなるのに全部で１８分かかったそうです。 　翌々日も同じ長さ（人数）の行列ができましたが、今度は行列の長さが３分の１になるまではマサルさんが、その後はトモエさんが応対したところ、行列がなくなるのに全部で２７分かかったそうです。 　では、行列の長さが３分の２になるまでは２人で、３分の１になるまではマサルさん１人で、行列がなくなるまではトモエさん１人で応対したとしたら、全部で何分かかっていたでしょうか。 （注）・・・売り場には開店後もどんどん並ぶ人が訪れています。また、そのペースは３日とも同じで一定であるものとします。

---

２．解答例１（長野美光さん、ありっちさん、すぐるくん、taroさん、ハラギャーテイさん、sekkiさん、ZZZZさん、ヒデー王子さん、他多数）

行列の３分の１を、マサル君、トモエさん２人で処理する場合、マサル君１人の場合、トモエさん１人の場合、それぞれの所要時間をt₁,t₂,t₃とします。
また、求める所要時間をtとします。

題意より、
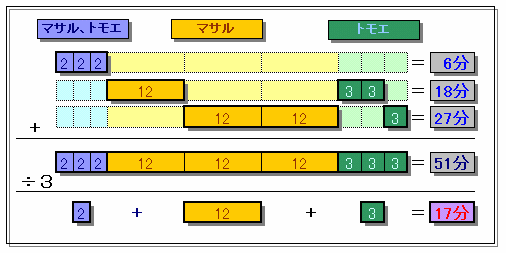
　　３t₁=６　・・・　（１）
　　ｔ₂＋２ｔ₃＝１８　・・・　（２）
　　２ｔ₂＋ｔ₃＝２７　・・・　（３）
　　t₁+t₂+t₃=t　・・・　（４）

（１）＋（２）＋（３）より、
　　３t₁+３t₂+３t₃=５１
よって、
　　ｔ＝t₁+t₂+t₃=５１/３＝１７

答：１７分

　以上

（参考）
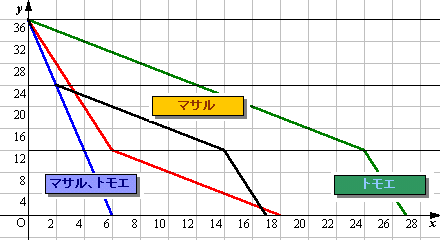
（１）、（２）、（３）を解くと、t1=２、t2=１２、t3=３を得ます。

ここで、行列人数、１分あたりマサル君１人の処理人数、トモエさん１人の処理人数、および新たに到着する人数を、それぞれＬ、a、b、cとすると、
　　Ｌ/3×（a+b-c）＝２　・・・　（５）
　　Ｌ/3×（a-c）=１２　　・・・　（６）
　　Ｌ/3×（b-c）=３　　　・・・　（７）
（５）、（６）、（７）より、
　　a = Ｌ×2/36, b=L×5／36、c = Ｌ×1/36
を得ます。

---