第２０５問の解答

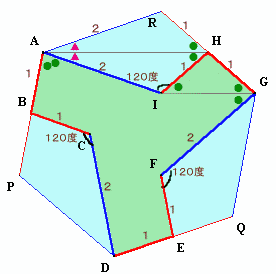
１．問題　［平面図形］

左図のような９角形ＡＢＣＤＥＦＧＨＩがあります。
ＡＩとＢＣ、ＤＣとＥＦ、ＧＦとＨＩが平行、角ＢＣＤ、角ＥＦＧ、角ＨＩＡは１２０゜になっています。
また、図の赤の辺と青の辺の長さの比はちょうど１：２になっています。

いま、ＩとＧ、ＡとＨをそれぞれ結んだところ、線分ＩＧと線分ＡＨも平行であったそうです。

では、９角形ＡＢＣＤＥＦＧＨＩの面積は、赤の辺（例えば辺ＡＢ）を一辺とする正三角形の何倍あるでしょうか。

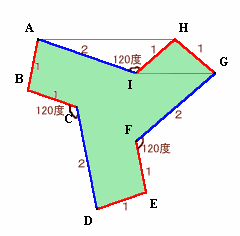２．解答例１（ＡЯＯＴさん、香川仁志さん、mitchさん、うっしーさん、他）

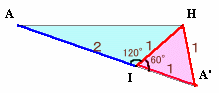
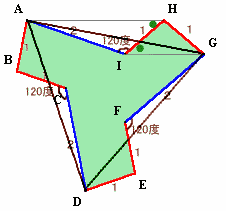
三角形ＡＩＨを折り返した三角形をＡＲＨとします。同様に、ＢＰＤ、ＥＱＧを作ります。

図１
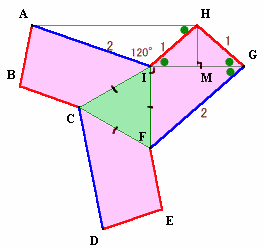
図２

このとき、ＡＰＤＱＧＲが正六角形となることを示します。

三角形ＨＩＧは、ＨＩ＝ＨＧの二等辺三角形だから∠ＨＩＧ＝∠ＨＧＩ。
この角をαとおきます。

ＡＨとＩＧが平行なことから、∠ＡＨＩ＝∠ＨＩＧ＝α。
△ＡＲＨと△ＡＩＨは合同だから、∠ＲＨＡ＝∠ＡＨＩ＝α。

∠ＲＨＡ＋∠ＡＨＩ＋∠ＩＨＧ＝２α＋∠ＩＨＧ＝１８０°（△ＨＩＧの内角の和）
よって、Ｇ、Ｈ、Ｒは一直線上に並ぶことが分かります。

また、ＨＩの長さを１とすると、ＧＲ＝ＲＡ＝２、∠ＡＲＨ＝∠ＡＩＨ＝１２０°。

さて、∠ＩＡＨ＝βとすると、∠ＲＡＨ＝β。
ＩＨとＦＧが平行より、∠ＨＩＧ＝∠ＩＧＦ＝α。

対象性より、∠ＢＡＩ＝∠ＨＧＦ＝２α。
よって、∠ＢＡＲ＝∠ＢＡＩ＋∠ＩＡＲ
　　＝２α＋２β＝２（α＋β）
　　＝２（∠ＩＡＨ＋∠ＩＨＡ）＝２（１８０°－∠ＡＩＨ）
　　＝２（１８０－１２０）＝１２０°。

同様にして、ＡＰＤＱＧＲの各辺の長さが２、頂点の内角が１２０度となることが分かるので、ＡＰＤＱＧＲは正六角形となります。

一辺が１の正三角形の面積＝Ｓとおきます。
正六角形ＡＰＤＱＧＲは、一辺が２の正三角形６個に分割されるので、面積は４Ｓ×６＝２４Ｓとなります。

また、図２のようにＡＩの延長線上にＩＡ'＝１となるよう点Ａ'をとると、
ＨＩ＝ＩＡ'＝１、∠ＨＩＡ'＝６０°より、△ＨＩＡ'は一辺が１の正三角形。
△ＡＩＨと△ＨＩＡ'は、高さが共通で底辺の長さが２：１。
よって、△ＡＩＨ＝２×△ＨＩＡ'＝２Ｓ。

したがって、求める９角形ＡＢＣＤＥＦＧＨＩの面積＝２４Ｓ－２Ｓ×６＝１２Ｓ。

答：１２倍

　以上

３．解答例２（中村明海さん、他）

三角形ＡＩＨを折り返した三角形をＡＲＨとします。同様に、ＢＰＤ、ＥＱＧを作ります。

対象性から、ＡＤＧは正三角形と考えられる。
また、△ＡＩＧ＝△ＨＩＧ等から、９角形ＡＢＣＤＥＦＧＨＩの面積＝△ＡＤＧとなります。

∠ＡＨＩ＝∠ＨＩＧ＝α、∠ＩＡＨ＝βとします。
△ＡＩＨについて、余弦定理より、
ＡＨ²＝ＡＩ²＋ＩＨ²－２×ＡＨ×ＩＨ×cos１２０°
　　　＝２²＋１²－２×２×１×１/２
　　　＝７
よって、ＡＨ＝√７。
また、正弦定理より、
ＡＨ／ｓｉｎ１２０°＝ＡＩ／ｓｉｎα＝ＩＨ／ｓｉｎβ、
ｓｉｎα＝ＡＩ／ＡＨ×ｓｉｎ１２０°
　　　＝２／√７×√３／２＝√３／√７。
ｃｏｓα＝√（１－ｓｉｎ²α）＝２／√７。
ｓｉｎβ＝ｓｉｎα×ＩＨ／ＡＩ＝√３／２√７。
ｃｏｓβ＝√（１－ｓｉｎ²β）＝５／２√７。

ＩＧ＝ＩＨ×ｃｏｓα×２＝１×２／√７×２＝４／√７。

△ＡＩＧについて、余弦定理より、
ＡＧ²＝ＡＩ²＋ＩＧ²－２×ＡＩ×ＩＧ×ｃｏｓ（１２０＋α）
　　　＝２²＋（４／√７）²－２×２×４／√７×ｃｏｓ（１８０－β）
　　　＝４＋１６／７＋１６／√７×５／２√７
　　　＝１２。

従って、９角形ＡＢＣＤＥＦＧＨＩの面積＝ＡＧ²×Ｓ＝１２Ｓ。

答：１２倍

第２０５問の解答

１．問題 ［平面図形］

２．解答例１（ＡЯＯＴさん、香川仁志さん、mitchさん、うっしーさん、他）

３．解答例２（中村明海さん、他）

４．解答例３

１．問題　［平面図形］