第２０６問の解答

１．問題　［整数の性質］

問題図
左図のような、縦３列、横３列のマス目があります。

　これらのマス目のＡ〜Ｉのそれぞれに、１〜９の９つの整数を書き込むことにします。
（同じ数を２度使うことはできません）
このとき、次の各問いに答えてください。

（１）縦・横・ナナメのどの方向についても、３つの整数の和が等しくなるような書き込み方は何通りあるでしょう？

（２）３ケタの整数ＡＢＣ、ＤＥＦ、ＧＨＩを考えます。
　ＤＥＦがＡＢＣの２倍、ＧＨＩがＡＢＣの３倍になっているような書き込み方のうち、ＡＢＣが最も大きくなる場合の整数ＡＢＣを答えてください。

２．解答例１（長野美光さん、萬田銀次郎さん、ταροさん、香川仁志さん、あんみつさん、AUさん、溝部光洋さん、M.Hossieさん、うっしーさん、他多数）

［設問１］

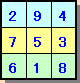
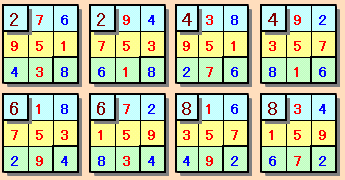
題意を満たすものは魔方陣と呼ばれ、３×３のものは回転、折り返し等を除き下記の１通りしかないことが知られています。

参考図1

従って、回転の４通り×折り返しの２通り＝８通りとなります。

（参考）上記１通りしかないこと

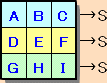
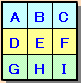
まず、縦・横・ナナメの３つの整数の和をＳとします。

参考図2

　　Ａ＋Ｂ＋Ｃ＝Ｓ　・・・　（１）
　　Ｄ＋Ｅ＋Ｆ＝Ｓ　・・・　（２）
　　Ｇ＋Ｈ＋Ｉ＝Ｓ　・・・　（３）

（１）＋（２）＋（３）より、
　　（Ａ＋Ｂ＋Ｃ）＋（Ｄ＋Ｅ＋Ｆ）＋（Ｇ＋Ｈ＋Ｉ）＝３Ｓ
　　１＋２＋３＋４＋５＋６＋７＋８＋９＝３Ｓ
　　４５＝３Ｓ
よって、Ｓ＝１５。

次に、真ん中のＥを求めます。

参考図3

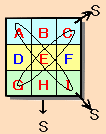
　　Ａ＋Ｅ＋Ｉ＝Ｓ　・・・　（４）
　　Ｃ＋Ｅ＋Ｇ＝Ｓ　・・・　（５）
　　Ｂ＋Ｅ＋Ｈ＝Ｓ　・・・　（６）

（４）＋（５）＋（６）より、
　　（Ａ＋Ｂ＋Ｃ）＋３Ｅ＋（Ｇ＋Ｈ＋Ｉ）＝３Ｓ
　　３Ｅ＝Ｓ
　　Ｅ＝Ｓ／３＝１５／３＝５。

さて、３つの整数を加えてＳ＝１５になるには、
　偶数＋偶数＋奇数、および奇数＋奇数＋奇数
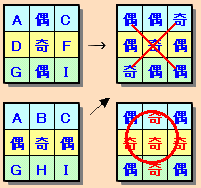
のどちらかのタイプとなります。

もし、真ん中の縦が、偶数＋偶数＋奇数のタイプと仮定すると、
各行とも偶数＋偶数＋奇数のタイプとなります。
ＡまたはＣのどちらかが偶数、残りが奇数となりますので、Ａが偶数、Ｃが奇数とすると、Ｄ，Ｆとも偶数なので、Ｇが奇数、Ｉが偶数となります。
すると、１から９までの整数の中に偶数が６個、奇数が３個となり不適。
Ａが奇数、Ｃが偶数の場合も同様。

また、もし、真ん中の横が、偶数＋偶数＋奇数のタイプと仮定しても全く同様に不適。

参考図4

よって、真ん中の縦・横とも奇数、４隅が偶数と分かります。

ここで、Ａが例えば２とすると、２＋５＋Ｉ＝１５より対角線のＩ＝８と決まります。
すると、Ｃ＝６、Ｇ＝４またはＣ＝４、Ｇ＝６の２通りとなり、４隅の偶数が決まれば残りの奇数は一意的に求まります。

参考図5


Ａは、２、４、６、８の４通りあるので、結局上記のように２×４＝８通りとなります。

［設問２］

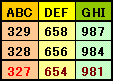
ABC×２＝ＤＥＦ、ＡＢＣ×３＝ＧＨＩで、ＧＨＩ≦９９９よりＡＢＣ≦３３３、
Ａ、Ｂ、Ｃは異なるのでＡＢＣ≦３２９。

そこで、ＡＢＣ＝３２９より順に小さくしていってABC×２、ＡＢＣ×３を計算していくと、ＡＢＣ＝３２７が題意を満たすことが分かるので、これが最大である。

参考図6

（参考）
ＡＢＣ、ＤＥＦ、ＧＨＩのそれぞれを９で割った余りは、Ａ＋Ｂ＋Ｃ、Ｄ＋Ｅ＋Ｆ、Ｇ＋Ｈ＋Ｉを９で割った余りと等しい。
よって、ＡＢＣ＋ＤＥＦ＋ＧＨＩ＝ＡＢＣ×６を９で割った余りは、（Ａ＋Ｂ＋Ｃ）＋（Ｄ＋Ｅ＋Ｆ）＋（Ｇ＋Ｈ＋Ｉ）＝４５を９で割った余り０と等しい。
これから、ＡＢＣは３の倍数であることが分かるので、３２７から順に３の倍数を調べていくと良いことが分かる。

なお、題意を満たす整数ＡＢＣは、大きい順に３２７、２７３、２１９、１９２の４通りです。

答：（１）８通り（２）３２７

　以上