第208問の解答
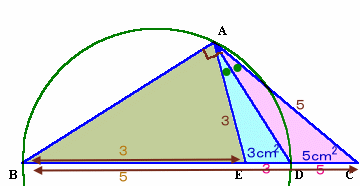
1.問題 [平面図形]
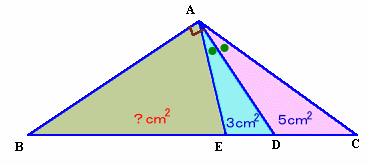 |
|
2.解答例1(長野美光さん、トトロ@Nさん、ταροさん、AЯOTさん、むらかみさん、他多数)
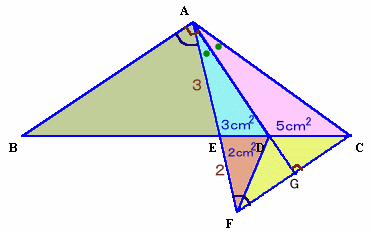
ADを軸として、△ACDを折り返し△AFDとする。
点Cと点Fを結び、辺CFと辺ADの延長線の交点をGとする。
△AFD=△ACD=5cm2、
△EFD=△AFD−△AED=5−3=2cm2。△AEDと△EFDは、高さが共通だから、面積の比は、底辺の比に等しい。
よって、AE:EF=△AED:△EFD=3:2。△AFGと△ACGは、AF=AC、AG共通、∠FAG=∠CAGより合同。
よって、FC⊥AG。AB⊥AGだから、AB//CF。
よって、∠BAF=∠AFC(錯角)。△ABEと△FCEについて、
∠BAE=∠AEC、∠AEB=∠FECより、△ABE∽△FCE。
よって、BE:EC=AE:EF=3:2。△ABEと△AECは、高さが共通だから面積比は底辺の比に等しい。
よって、△ABE:△AEC=AE:EF=3:2。
従って、△ABE=△AEC×3/2=8×3/2=12cm2。答:12cm2
以上
3.解答例2(うっしーさん、やさん、清川育男さん、なおぞうさん、他)
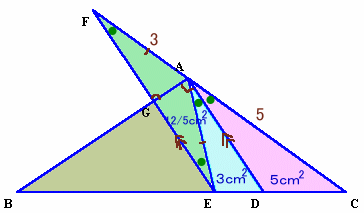
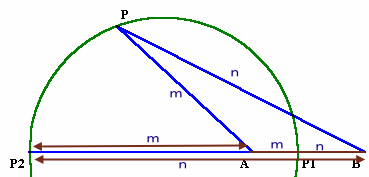
点Eを通り、ADに平行な直線と、CAの延長との交点をFとする。
AD//FEより、∠DAE=∠AEF(錯角) 、∠CAD=∠AFE(同位角)、
題意より∠DAE=∠CAD。
よっって、∠AEF=∠AFE 。
よって、△AEFは二等辺三角形。AE=AF 。解答例と同様にして、AE:AC=△AED:△ACD=3:5。
AE=AFより、AF:AC=3:5。△FEC:△AEC=FC:AC=8:5。
よって、△AFE:△AEC=3:5。
従って、△AFE=△AEC×3/5=8×3/5=24/5cm2。FE//ADでAB⊥ADより、AB⊥FE。
ABとEFとの交点をGとする。
△AEG=△AFE×1/2=12/5cm2。△AEGと△AEDの高さはAGで共通だから、
EG:AD=△AEG:△AED=12/5:3=4:5。
FE//ADより、BE:BD=GE:AD=4:5、
よって、BE:ED=4:1となる。△ABE:△AED=BE:ED=4:1、
よって、△ABE=△AED×4=3×4=12cm2となる。
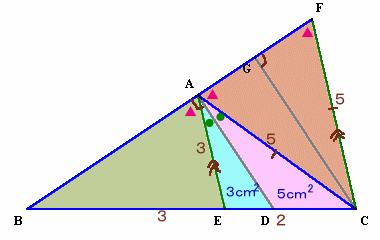
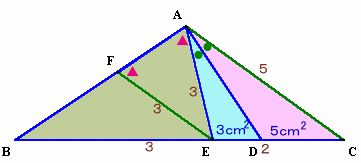
4.解答例3(げんさん、他)
点Cから辺EAに平行な直線を引き、BAとの延長との交点をFとし、
点CからADに平行な直線を引き、BFとの交点をGとする。