第２０９問の解答

１．問題　［立体図形］

問題図
　左図のような正四面体ＡＢＣＤがあります。この正四面体を、
　　・ＡＢを含み、四面体ＡＢＣＤの体積を二等分する平面
　　・ＢＣを含み、四面体ＡＢＣＤの体積を二等分する平面
　　・ＣＡを含み、四面体ＡＢＣＤの体積を二等分する平面
の３つの平面で切断します。（３回の切断が終わるまで、立体は動かないものとします）

このとき、
　・正四面体は何個の立体に分割されるでしょうか？
　・また、分割後の立体を体積を同じ大きさのものはひとつのグループ
　　にして比較すると、最も大きいグループと２番目に大きいグループ
　　に属する立体の体積比は何：何になるでしょう。

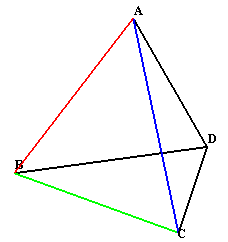２．解答例１（マサルさん、香川仁志さん、他）

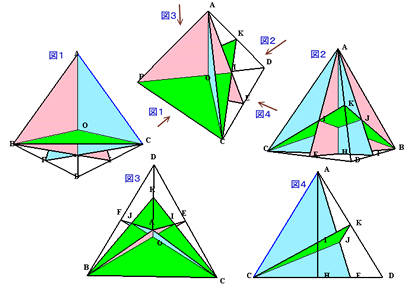
切断面が見えやすいよう、正四面体AＢCDの各面を透過してみると下図のようになります。

参考図1
(JavaAppletによる動く３Ｄ図)

まず、１回の切断で２つの立体に分割されるため、３回の切断では、２3＝８個の立体に分割されます。

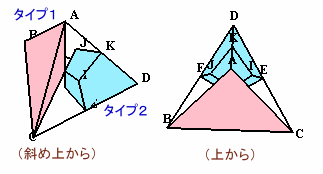
これら８個の立体はよく見ると４つのタイプに分類されます。

参考図2 参考図5
（タイプ１、タイプ２をそれぞれ３等分）
タイプ１：
△ＡＢＣと中心Ｏを結んでできる正三角錐。
体積は、正四面体の1/4。		 タイプ２：
３等分するとタイプ４と同じ四角錐になる。
体積は、正四面体の1/4。
参考図3
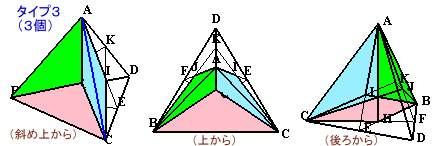タイプ３：
タイプ１を３等分したものと同じ三角錐。
体積は、正四面体の1/12。
参考図4
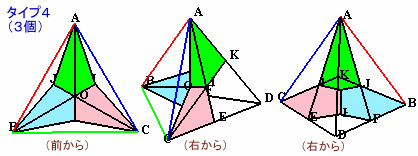タイプ４：
四角錐で、縦に切断して２等分すると、タイプ３を２等分したものと同じ大きさの三角錐になる。
体積は、正四面体の1/12。

よって、体積の大きさで分けると、
　・タイプ１、タイプ２：正四面体の1/4　（合計２個）
　・タイプ３、タイプ４：正四面体の1/１２（合計６個）
となります。
よって、求める体積比は、1/4：1/12＝３：１になります。

答：８個、３：１

　以上

３．解答例２（うっしーさん、他）

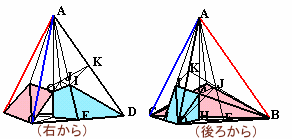
平面ＡＢＥで２等分してできる、２つの三角錐C-BEA、A-BEDについて、それぞれを構成する４つの立体の体積比を求めましょう。

図５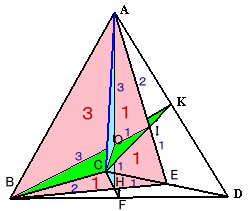
参考図6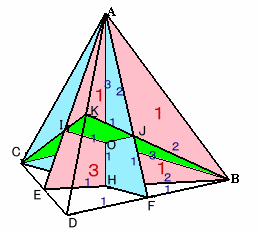		 図６
参考図7

図５で、三角錐C-BEAの分割した４つの立体は、Ｃを頂点とする高さが共通なので、体積比は底面の面積比に等しい。
ＢＨ：ＨＥ＝２：１より、△ＡＢＨ：△ＡＨＥ＝２：１。・・・（１）
ＡＯ：ＯＨ＝３：１より、△ＡＢＯ：△ＯＢＨ＝３：１。・・・（２）
ＡＯ：ＯＨ＝３：１、ＡＩ：ＩＥ＝２：１より、
　　△ＡＯＩ/△ＡＨＥ＝３／４×２／３＝１／２。
よって、△ＡＯＩ：四角形ＩＯＨＥ＝１：１。・・・（３）

（１）、（２）、（３）より、
　　△ＡＢＯ：△ＯＢＨ：△ＡＯＩ：四角形ＩＯＨＥ＝３：１：１：１。
従って、４つの立体の体積も３：１：１：１。・・・（４）

図６で、まず三角錐A-BEDを平面ＡＨＦで四角錐A-EDFH、三角錐A-HFBに分割する。
高さが共通だから、体積比は底面の面積比に等しい。
ＤＦ：ＦＢ＝１：１、ＥＨ：ＨＢ＝２：１より、
　　△ＢＨＦ／△ＢＥＤ＝２／３×１／２＝１／３、
よって、四角錐A-EDFH：三角錐A-HFB＝２：１。・・・（５）

三角錐A-HFBを底面がＡＨＦで頂点がＢの三角錐とみると、これを平面ＢＯＪで分割してできる立体の体積比は、底面の比に等しい。
ＡＯ：ＯＨ＝３：１、ＡＪ：ＪＦ＝２：１より、
　　△ＡＯＪ/△ＡＨＦ＝３／４×２／３＝１／２。
よって、△ＡＯＪ：四角形ＪＯＨＦ＝１：１。
従って、三角錐B-AOJ：四角錐B-JOHF＝１：１。・・・（６）

同様に、三角錐B-AIKを平面AＯＪで分割してできる立体の体積比は、底面の比に等しい。
BＯ：ＯI＝３：１、BJ：JK＝２：１より、
　　△BＯＪ/△BIK＝３／４×２／３＝１／２。
よって、△BＯＪ：四角形ＪＯKI＝１：１。
従って、三角錐B-AOJ：四角錐A-JOKI＝１：１。・・・（７）

（５）、（６）、（７）より、　　
　　６面体ＪＯKI−JOHF：四角錐B-JOHF＝３：１。
従って、４つの立体の体積比も３：１：１：１。・・・（８）

（４）、（８）、および２つの三角錐C-BEAとA-BEDの体積は等しいことから、
結局８つの立体は、体積３のものが２個、体積１のものが６個となる。

よって、求める立体の個数、体積比は８個、および３：１となる。