第210問の解答
1.問題 [速さの問題]
| ある駅の構内には、「動く歩道」が設置されていて、 P地点からQ地点に向かって動いています。 いま、P地点からトモエさんが、Q地点からマサルさんが同時に出発します。 2人は、同じ速さで動く歩道上を歩いています。(※) 2人は、出会うとすぐに「回れ右」をして歩き出します。 そして、出発点に着くとまた「回れ右」をして歩き出します。 これを何度も繰り返したところ、トモエさんがはじめてP地点に戻ったのは12分後、 マサルさんが2度目にQ地点に戻ったのは18分後であったそうです。 では、2人が3回目に出会うのは何分後でしょう? ※・・・・・2人の歩く速さは、動く歩道よりも速いものとします。 ※・・・・・「同じ速さで」とは、普通の地面の上で同じ速さ、という意味です。 |
2.解答例1(杉本未来さん、ヒデー王子さん、香川仁志さん、ふきゅさん、すぐるくん、H.Takaiさん、圭太さん、長野美光さん、ありっちさん、TORAさん、M.Hossieさん、他多数)
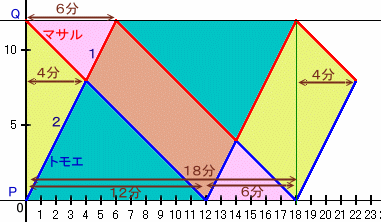
下図のようにダイアグラムを描きます。
二人が地上では同じ速度で歩くので、二人のP→Q、Q→Pの速度も同じ。
従って、
・トモエさんが最初にP地点へ戻るに要した12分は、
Q→Pに要する時間と同じ
・マサルさんが2度目にQ地点へ戻るに要した18分は、
二人がPQ間を一往復に要する時間と同じ
になります。
これから、P→Qに要する時間は18−12=6分と分かります。また、二人がPQ間を一往復した18分後から、3度目に出会うまでの時間は、ちょうど出発して最初に二人が出会うまでの時間に等しい。
上図より、P→Q:Q→P=12:6=2:1。
よって、出会うまでの時間は、6×2/3=4分となります。従って、3度目に出会うのは、18+4=22分後ということになります。
答:22分後
以上