第２１７問の解答

---

１．問題　［平面図形］

正六角柱ＡＢＣＤＥＦ−ＧＨＩＪＫＬがあります。この正六角柱は、底面は正六角形、側面は正方形でできています。 　左図は、この正六角柱上の点Ｃと点Ｆを赤い糸で結んだところを表したところで、赤い糸は辺ＨＩ上の点Ｐ、辺ＫＬ上の点Ｑを通っており、糸の長さが最も短くなるようにピンと張られています。 　この糸の長さを測ったところ、１６cmであったそうです。 　このとき、この正六角柱の表面積は何cm2でしょうか。

---

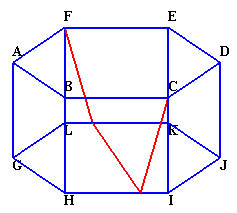２．解答例１（長野美光さん、ヒデー王子さん、ぶぶおパパさん、あすとさん、香川仁志さん、ταροさん、CRYING DOLPHINさん、H.Takaiさん、アーチャンさん、航介さん、圭太さん、谷口英之さん、あやのりんさん、okaokaさん、トトロ＠Ｎさん、ありっちさん、他多数）

図１のような展開図を考えます。

図１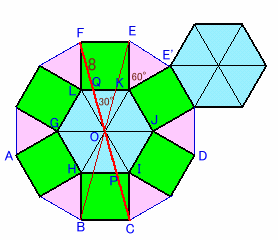

図２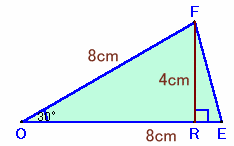

正方形と正方形のすきまにできる２等辺三角形は、頂角が
　　３６０−（６０×２＋９０×２）＝６０°
となるので、正六角形を６等分してできる正三角形とちょうど同じ大きさの正三角形になります。

よって、求める正六角柱の表面積は、図１のように対角線の長さがちょうど問題の赤い糸の長さと同じ１６ｃｍである正１２角形の面積に等しくなります。

この正１２角形の１２分の１である２等辺三角形は、図２のように頂角が３６０／１２＝３０°で、それをはさむ２辺の長さが１６／２＝８ｃｍになります。
また、この三角形の高さは、８／２＝４ｃｍなので、面積は1/2×８×４＝１６cm²。

よって、求める表面積は、１６×１２＝１９２cm²となります。

答 １９２cm²

　以上

---

３．解答例２（ありっちさん、長野美光さん、高田修成さん、圭太さん、Ogihさん、中村明海さん、ハラギャーテイさん、M.Hossieさん、高橋道広さん、ほそたにさん、他多数）

下図の展開図で正方形の１辺の長さをaとします。

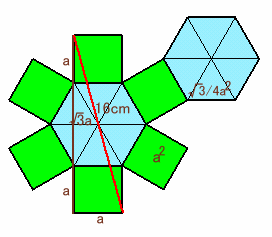
題意より、赤い糸の長さ１６ｃｍを斜辺とする直角三角形の１辺がａ、もう１辺が（２＋√3）aとなります。

よって、ピタゴラスの定理より、
　　a²＋{（２＋√3）a}²＝１６²、
　　（8＋4√3）a²＝１６²、
よって、
　　（２＋√3）a²＝１６×４。

求める表面積は、正方形６個、正三角形１２個の面積に等しいので、
　　　a²×６＋√3/4a²×１２
　＝３（２＋√3）a²
　＝１６×１２
　＝１９２cm²。

---