第２１８問の解答

１．問題　［平面図形］

問題図
左図のような５角形ＡＢＣＤＥがあります。
この５角形は、
　・∠ＢＣＤ＝９０゜
　・∠ＢＡＣ（●）＋∠ＣＥＤ（▲）＝９０゜
　・∠ＤＢＣ（■）×２＝∠ＣＤＥ（■■）
という特徴があり、さらに
　・ＡＢ＋ＢＣ＝１２cm
　・ＥＤ＋ＤＣ＝　７cm
　・△ＢＣＤ＝１０cm2
　となっています。

では、この五角形ＡＢＣＤＥの面積は何cm2でしょうか。

　

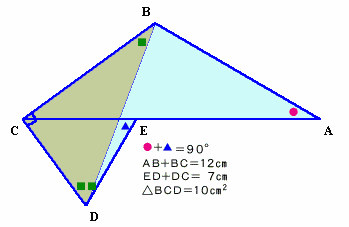２．解答例１（香川仁志さん、M.Hossieさん、うっしーさん、他多数）

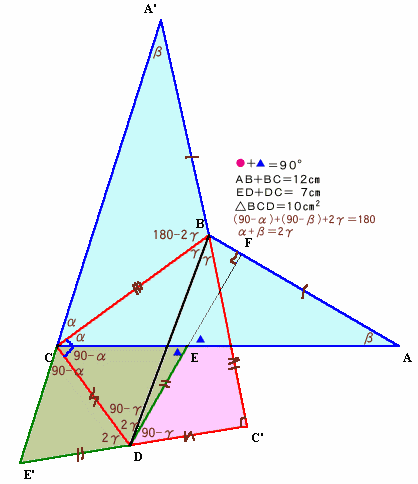
△ＡBCを、BCを軸として折り返したものを△Ａ’ＢＣ、
△ＣＤＥを、ＣＤを軸として折り返したものを△ＣＤＥ’、
△BCＤを、BＤを軸として折り返したものを△ＢＣ’Ｄとします。

参考図1

Ａ’ＢＣ’、Ａ’ＣＥ’、Ｃ’ＤＥ’は、それぞれ一直線をなすことを示します。
∠ＢＣＤ＝α、∠ＢＡＣ＝β、∠ＣＢＤ＝γとします。
題意より、∠ＣＤＥ＝２γ、∠ＡＣＤ＝９０−α、∠ＣＥＤ＝９０−β。
よって、（９０−α）＋（９０−β）＋２γ＝１８０、
従って、α＋β＝２γ。　・・・　（１）

△Ａ’ＢＣで、∠Ａ’ＣＢ＝∠ＡＣＢ＝α、∠ＢＡ’Ｃ＝∠ＢＡＣ＝β、
よって、∠Ａ’ＢＣ＝１８０−（α＋β）＝１８０−２γ。
また、∠Ｃ’ＢＤ＝∠ＣＢＤ＝γ。
よって、
∠Ａ’ＢＣ＋∠ＣＢＤ＋∠Ｃ’ＢＤ＝（１８０−２γ）＋γ＋γ＝１８０°、
従って、Ａ’ＢＣ’は、一直線をなすことになります。

△ＣＤＥ’で、∠Ｅ’ＣＤ＝∠ＥＣＤ＝９０−α、∠ＣＤＥ’＝∠ＣＤＥ＝２γ、
よって、∠Ａ’ＣＢ＋∠ＢＣＤ＋∠Ｅ’ＣＤ＝α＋９０＋（９０−α）＝１８０°、
従って、ＣＤＥ’は、一直線をなすことになります。

また、∠Ｃ’ＤＢ＝∠ＣＤＢ＝９０−２γ、
よって、∠ＣＤＥ’＋∠ＣＤＢ＋∠Ｃ’ＤＢ
　　＝２γ＋（９０−２γ）＋（９０−２γ）＝１８０°、
従って、ＣＤＥ’は、一直線をなすことになります。

さて、△Ａ’Ｃ’Ｅ’について、
　Ａ’Ｃ’＝Ａ’Ｂ＋ＢＣ’＝ＡＢ＋ＢＣ＝１２ｃｍ、
　Ｃ’Ｅ’＝Ｃ’Ｄ＋ＤＥ’＝ＣＤ＋ＤＥ＝７ｃｍ、
　∠Ａ’ＣＥ’＝∠ＡＣＥ＝９０°、
より、直角三角形となるので面積は、1/2×７×１２＝４２ｃｍ2。

△Ａ’Ｃ’Ｅ’＝△Ａ’ＢＣ＋△ＣＤＥ’＋２△ＢＣＤ、
よって、五角形ＡＢＣＤＥ
　＝△ＡＢＣ＋△ＣＤＥ
　＝△Ａ’ＢＣ＋△ＣＤＥ’
　＝△Ａ’Ｃ’Ｅ’−２△ＢＣＤ
　＝４２−２×１０
　＝２２ｃｍ2
となります。

答 ２２cm2

　以上

３．解答例２（武田浩紀さん、他）

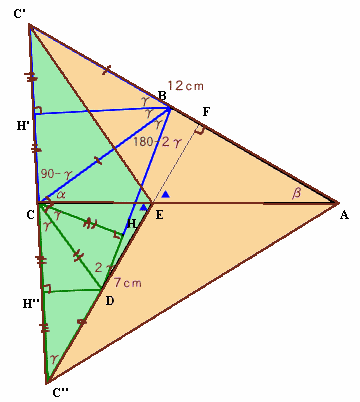
ＡＢを延長しＢＣ’＝ＢＣ、およびＥＤを延長してＤＣ’’＝ＤＣとします。
また、ＤＥの延長とＡＢの交点をＦ、およびＣからＢＤに下ろした垂線の足をＨとします。
さらに、ＣとＣ’、ＣとＣ’’を結び、ＢからＣＣ’に、およびＤからＣＣ’’に下ろした垂線の足をＨ’、Ｈ’’とします。

参考図2

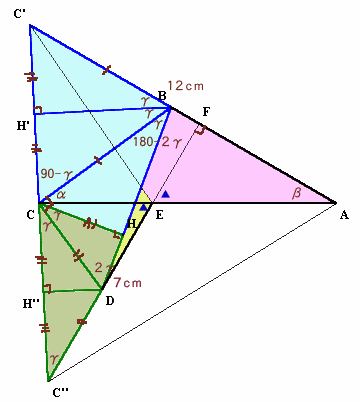
Ｃ’、Ｃ、Ｃ’’が一直線上にあり、ＣＣ’＝ＣＣ’’なることを示しましょう。

題意より、∠ＡＦＥ＝１８０−（∠ＡＥＦ＋∠ＦＡＥ）＝１８０−９０＝９０°。
四角形ＢＣＤＦについて、∠ＢＣＤ＝∠ＡＦＥ＝９０°、
よって、
　∠ＣＢＦ＝１８０−∠ＣＤＦ＝１８０−２γ、
　∠ＣＢＣ’＝１８０−∠ＣＢＦ＝２γ
となります。

直角三角形△ＢＣＨ’と△ＢＣ’Ｈ’について、
　ＢＣ＝ＢＣ’、ＢＨ’は共通より、
　△ＢＣＨ’≡△ＢＣ’Ｈ’。
よって、ＣＨ’＝Ｃ’Ｈ’　・・・　（１）
また、∠ＣＢＨ’＝∠Ｃ’ＢＨ’＝∠ＣＤＦ／２＝２γ／２＝γ、
　∠ＢＣＨ’＝９０−γ。　・・・　（２）

直角三角形△ＢＣＨと△ＢＣＨ’について、
　ＢＣ＝ＢＣ’、∠ＣＢＨ＝∠Ｃ’ＢＨ＝γより、
　△ＢＣＨ≡△ＢＣ’Ｈ’。
よって、ＣＨ＝ＣＨ’　・・・　（３）

また、△ＣＤＨについて、∠ＤＣＨ＝９０−∠ＢＤＣ＝∠ＣＢＤ＝γ。

次に、直角三角形△ＤＣＨ’’と△ＤＣ’’Ｈ’’について、
　∠ＤＣＨ＝∠ＤＣＨ’’＝γ、ＤＣ共通より、
　△ＤＣＨ’’≡△ＤＣ’’Ｈ’。
よって、ＣＨ’’＝Ｃ’’Ｈ’’　・・・　（４）
　∠ＤＣＨ’’＝∠ＤＣ’’Ｈ’’＝∠ＣＤＦ／２＝γ　　・・・　（５）

直角三角形△ＤＣＨと△ＤＣＨ’’について、
　ＤＣ＝ＤＣ’’、ＤＨ’’は共通より、
　△ＤＣＨ≡△ＤＣＨ’’。
よって、ＣＨ＝ＣＨ’’　・・・　（６）

（１）、（３）、（４）、（６）より、
　ＣＣ’＝２ＣＨ’＝２ＣＨ’’＝ＣＣ’’　・・・　（７）
（２）、（５）より、
　∠Ｃ’ＣＢ＋∠ＢＣＤ＋∠Ｃ’’ＣＤ＝（９０−γ）＋９０＋γ＝１８０、
よって、Ｃ’、Ｃ、Ｃ’’は一直線上にある。

参考図3

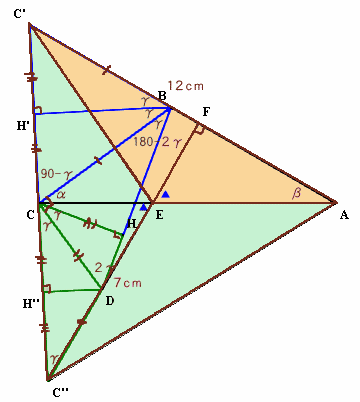
さて、四角形Ｃ’ＣＡＥ
　＝△Ｃ’Ｃ’’Ａ−△Ｃ’ＥＡ
　＝1/2×Ｃ’’Ｆ×ＡＣ’−1/2×ＥＦ×ＡＣ’
　＝1/2×Ｃ’’Ｅ×ＡＣ’

Ｃ’’Ｅ＝Ｃ’’Ｄ＋ＤＥ＝ＣＤ＋ＤＥ＝７ｃｍ、
ＡＣ’＝ＡＢ＋ＢＣ’＝ＡＢ＋ＢＣ＝１２ｃｍ。

よって、四角形Ｃ’Ｃ’’ＥＡ＝1/2×７×１２＝４２ｃｍ2。・・・　（８）

参考図4

△ＡＣ’Ｅ＝△ＡＣ’Ｃ−△ＥＣ’Ｃ、
△ＡＣ’’Ｅ＝△ＡＣ’’Ｃ−△ＥＣ’’Ｃ。

△ＡＣ’Ｃと△ＡＣ’’Ｃは、高さが共通で、底辺がＣＣ’＝ＣＣ’’、
よって△ＡＣ’Ｃと△ＡＣ’’Ｃ。

△ＥＣ’Ｃと△ＥＣ’’Ｃは、高さが共通で、底辺がＣＣ’＝ＣＣ’’、
よって△ＥＣ’Ｃと△ＥＣ’’Ｃ。

従って、△ＡＣ’Ｅ＝△ＡＣ’’Ｅ。・・・　（９）

よって（８）、（９）より、
　四角形ＡＣ’Ｃ’’Ｅ
　＝△ＡＣ’Ｅ＋△Ｃ’Ｃ’’Ｅ
　＝△ＡＣ’’Ｅ＋△Ｃ’Ｃ’’Ｅ
　＝四角形Ｃ’Ｃ’’ＥＡ
　＝４２ｃｍ2。・・・　（１０）

五角形ＡＢＣＤＥ
　＝△ＡＢＣ＋△ＣＤＥ
　＝（△ＡＣＣ’−△ＢＣＣ’）＋（△ＥＣＣ’’−△ＣＤＣ’’）
　＝（△ＡＣＣ’＋△ＥＣＣ’’）−（△ＢＣＣ’＋△ＣＤＣ’’）
　＝四角形ＡＣ’Ｃ’’Ｅ−ＢＣＤ×２
　＝４２−１０×２　　←（１０）より
　＝２２ｃｍ2。