第２１９問の解答

---

１．問題　［空間図形、規則性］

マサル商店が開発した新製品は、「くっついているボールの数を表示する」という性質を持った不思議なボールです。 例えば、図１のように２個のボールをくっつけると、どちらも「１」と表示されます。図２のように３個のボールを一列に並べてくっつけると、両端のボールは「１」、真ん中のボールは「２」と表示するわけです。 いま、このボールを図３のように１段目には１個のボールを置き、２段目は１辺がボール２個でできた正三角形状に並べて置き、３段目は一辺がボール３個でできた正三角形状に置き、・・・・・というようにボールを重ねていきます。（※）（図３には４段目までのとき）このとき、各ボールはそれぞれにくっついているボールの数を表示しています。 いま、ある段数まで重ねたところ、全てのボールに表示されている数の合計が１００８になりました。 このとき、ボールは何個使ったでしょうか。 ※・・・正三角形状に並べる際に、各ボールがくっつくようにします。（図３の内部にもボールは詰まっています）

---

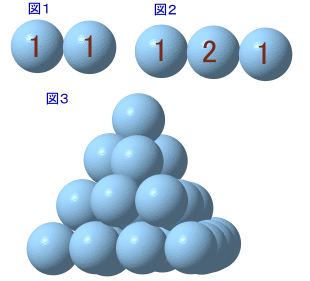２．解答例１（ふぇるまーさん、ＡЯＯＴさん、まるケンさん、M.Hossieさん、井合宗太郎さん、他多数）

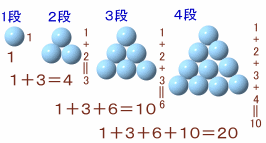
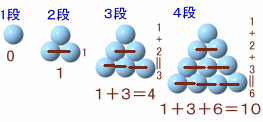
段数をｎとし、ボールの個数をカウントします。

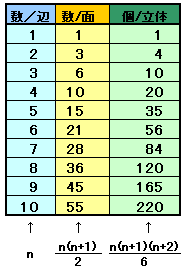
１辺にある個数は、段数ｎが増えるたびに１、２、３、・・・、と１個ずつ増えていくので、ｎ段でｎ個。

１面にある個数f(n)は、ｎが増えるたびに１辺上の個数だけ増えていくので、
順次足していくと１、３、６、・・・、となり、一般式ではn(n+1)/2個。

f(n)=Σk=1+2+・・・+n=n+・・・+2+1
2f(n)=(n+)+(n+1)+・・・+(n+1)=n(n+1)
よって、f(n)=n(n+1)/2

立体上にある個数s(n)は、ｎが増えるたびに１面上の個数だけ増えていくので、
順次足していくと１、４、１０、・・・、となり、一般式ではn(n+1)(n+2)/6個と表される。

n³-(n-1)³=3n²-3n+1
Σk³-Σ(k-1)³=3Σk²-3Σk+Σ1
n³-0³=3Σk²-3n(n+1)/2+n
よって、Σk²={n³+3n(n+1)/2-n}/3=n(n+1)(2n+1)/6
s(n)=Σk(k+1)=Σk²+Σk=n(n+1)(2n+1)/6+n(n+1)/2=n(n+1)(n+2)/6

ここまでは、各解答例で共通です。

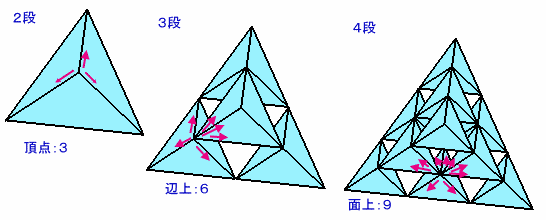
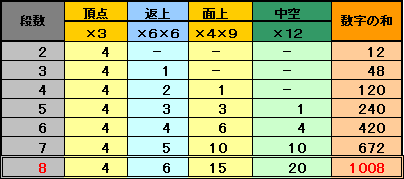
次にボールが頂点、辺上（頂点を除く）、面上（返上を除く）、中空部分の各部分にあるとき、数字は３、６、９、１２となることが分かります。

・２段のとき 　頂点が４個×３＝１２ ・３段のとき 　頂点が４個×３＝１２ 　辺上が１×６個×６＝３６　計４８ ・４段のとき 　頂点が４個×３＝１２ 　辺上が２×６個×６＝７２ 　面上が１×４個×９＝３６　計１２０ ・５段のとき 　頂点が４個×３＝１２ 　辺上が３×６個×６＝１０８ 　面上が３×４個×９＝３６ 　中空が１個×１２＝１２　　計２４０

・６段のとき 　頂点が４個×３＝１２ 　辺上が４×６個×６＝１０８ 　面上が６×４個×９＝３６ 　中空が４個×１２＝１２　　計４２０ ・７段のとき 　頂点が４個×３＝１２ 　辺上が５×６個×６＝１０８ 　面上が１０×４個×９＝３６ 　中空が１０個×１２＝１２　計６７２ ・８段のとき 　頂点が４個×３＝１２ 　辺上が６×６個×６＝１０８ 　面上が１５×４個×９＝３６ 　中空が２０個×１２＝１２　計１００８

式で表すと、
　数字の和
＝4×3＋(n-2)×36＋(n-3)(n-2)/2×36＋(n-4)(n-3)(n-2)/6×12
＝2(n-1)n(n+1)

よって、段数は８と分かるので、このときボールの数は１２０個となります。

答 １２０個

　以上

---

３．解答例２（マサルさん、他）

求める数字の和は、隣り合うボールの中心を結ぶ線分の個数を求めれば、その２倍となります。

ここで線分の向きは正四面体の辺の数の６通りあります。
１つの向きの線分を考えると、各列ではボールの数より１個少ないので、
全体としては１段少ない立体のボール数に等しい。

数字の和は、この６×２＝１２倍となるので、

ｎ＝２のとき、　１×１２＝　１２ ｎ＝３のとき、　４×１２＝　４８ ｎ＝４のとき、１０×１２＝１２０ ｎ＝５のとき、２０×１２＝２４０

ｎ＝６のとき、３５×１２＝　４２０ ｎ＝７のとき、５６×１２＝　６７２ ｎ＝８のとき、８４×１２＝１００８

よって、段数は８、ボールの数は１２０個となる。

数式で表すと、ｎ段のときのボール数をＮ（n）＝n(n+1)(n+2)/6。
Ｓ（ｎ−１）×１２＝(n-1)n(n+1)/6×１２＝2(n-1)n(n+1)となります。

以下同様

---

４．解答例３（げんさん、ありっちさん、たなかさん、noetherさん、ταροさん、有無相生さん、他）

解答例２同様線分の数の２倍で求めます。
ｎ段のときの線分の数をg(n)とします。

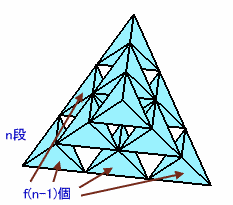
上図より、(n-1)段からｎ段に増えるとき、増加する線分の数は、
(n-1)段目のボールの下に正四面体をくっつけたと考えられるので、
　　g(n)-g(n-1)=6f(n-1)
　　Σg(k)-Σg(k-1)=Σf(k-1)
　　g(n)-g(0)=6s(n)=(n-1)n(n+1) (g(0)=0とする）
よって、求める数字の和は、2g(n)=(n-1)n(n+1)

以下同様

---