第２２１問の解答

１．問題　［平面図形］

問題図
Ａ、Ｂ、Ｃ、Ｄの４本のクイが打たれています。
ロープでＡ、Ｂ、Ｃを結んだところ、その形は正三角形になりました。
Ａ、Ｂ、Ｄを結んだところ、角ＡＤＢは６０゜となり、ロープの長さは１８ｍでした。
Ｂ、Ｃ、Ｄを結んだところ、ロープの長さは１５ｍでした。
Ａ、Ｃ、Ｄを結んだところ、角ＡＤＣは６０゜となり、ロープの長さは２０ｍでした。

このとき、
（１）ＡＤ間の距離は何ｍでしょうか。
（２）正三角形ＡＢＣと三角形ＢＣＤの面積比は何対何でしょうか。

　

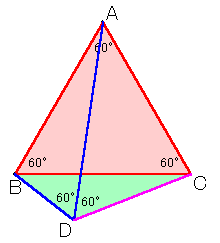２．解答例１（ヒデー王子さん、DrKさん、ＫＩＮさん、noetherさん、dragon-kさん、M.Hossieさん、航介さん、他多数）

AB=BC=CA=a、BD=b、CD=c、AD=dとします。

参考図1

題意より、
　a＋b＋c　　＝15　・・・　（１）
　a＋b　　＋d＝18　・・・　（２）
　a　　＋c＋d＝20　・・・　（３）
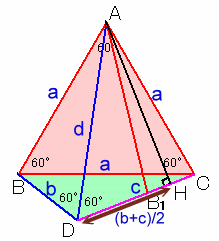
が成り立つ。

また、ADを軸に△ABDを折り返し△ＡＢ1Ｄとする。
∠ADB=∠ADB1＝６０度だから、B1は辺ＣＤ上にある。

Ａから辺CDに下ろした垂線の足をHとすると、∠ADC=６０度より、
　DH=（b＋ｃ）/２＝d/２
よって、b＋c＝d　・・・　（４）

（２）＋（３）＋（４）より、
　2a＋2b＋2c＋2d＝38＋d
（１）より、
　30＋2d＝38＋d
よって、d＝8。

（４）より、b＋c＝8　・・・　（５）

（１）−（５）より、a＝7。
（２）より、b＝18−(a＋d)＝3。
（３）より、c＝20−(a＋d)＝5。

従って、a＝7、b＝3、c＝5、d＝8を得る。

さて、△ABC＝1/2×a2×cos(60度)、
　　　△BCD＝1/2×bc×cos(60度)より、
△ABC：△BCD＝a2：bc＝49：15となる。

答 ３３６ｍ

　以上

３．解答例２（ταροさん、C-Dさん、萬田銀次郎さん、うっしーさん、ありっちさん、あんみつさん、香川仁志さん、noetherさん、YokoyaMacさん、POIさん、他）

b＋c＝dを別の方法で求めます。
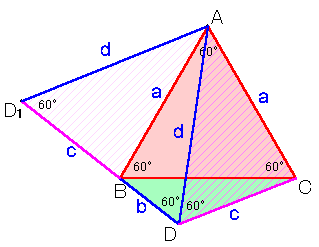
△ACDを６０度回転したものを△ＡＢＤ1とします。

参考図2

∠ABD＝∠ACD＝６０度＋∠BCD、
よって、
　∠ABD＋∠ABC＋∠CBD
＝（６０度＋∠BCD）＋６０度＋∠CBD
＝∠BCD＋∠CBD＋１２０度
＝１８０度。
従って、D1BDは一直線上にある。

AD1＝AD=d、
∠D1AD＝∠D1AB＋∠BAD＝∠DAC＋∠BAD＝６０度。
よって、△AD1Dは正三角形となる。
従って、D1D＝b＋c＝AD＝dとなる。

以下、解答例１と同様。

４．解答例３

b＋c＝dを別の方法で求めます。
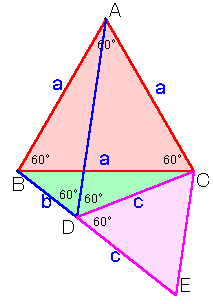
BDを延長し、DE=DC＝cとします。

参考図3

∠CDE＝１８０−１２０＝６０度、ＤＥ＝ＤＣだから、△ＣＤＥは正三角形。
よって、ＣＥ＝DC。
△ＢＣＥと△ＡＣＤについて、
ＢＣ＝ＡＣ＝ａ、ＣＥ＝ＤＣ＝ｃ、∠ＢＣＥ＝∠ＢＣＤ＋６０度＝∠ＡＣＤ、
よって、△ＢＣＥ≡△ＡＣＤ。
従って、ＢＥ＝ｂ＋ｃ＝ＡＤ＝ｄ。

５．解答例４（マサルさん、他）

b＋c＝dを別の方法で求めます。
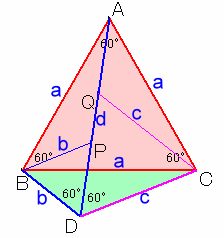
AD上にＰＤ＝ＢＤ、QD=CDとなるよう点Ｐ、Ｑを取ります。

参考図4

△ＢＤＰ、△ＣＤＱは、それぞれ正三角形になります。

△ＡＢＰと△ＣＢＤについて、
ＡＢ＝ＣＢ＝ａ、ＢＰ＝ＢＤ＝ｂ、∠ＡＢＰ＝６０−∠ＰＢＣ＝∠ＣＢＤより、
△ＡＢＰ≡△ＣＢＤ。
従って、ＡＰ＝ＣＤ＝ｃ。

よって、ＡＤ＝ｄ＝ＡＰ＋ＰＤ＝ｃ＋ｂ。

さらに、△ＡＢＣ＝Ｓ１、△ＢＣＤ＝Ｓ２とすると、
Ｓ１＋Ｓ２＝△ＡＢＤ＋△ＡＣＤ＝２Ｓ２＋Ｓ１×（b/a）2＋Ｓ１×（c/a）2、
Ｓ１×（a2-b2-c2）/a2＝Ｓ２、
よって、Ｓ１：Ｓ２＝a2：（a2-b2-c2）＝４９：１５。

（その他の解答例）

・Gouさん、ふぇるまーさん、ハラギャーテイさん
△AＢＤについて、余弦定理より、
　a2＝b2＋d2−2bd・cos60度＝b2＋d2−bd　・・・（１）
△AＣＤについて、余弦定理より、
　a2＝c2＋d2−2cd・cos120度＝c2＋d2−cd　・・・（２）

（１）−（２）より、
　b2−c2−bd＋cd＝0、
　（b-c）（b＋c−d）＝0、
よって、b＝c、またはb＋c＝d。

b＝cは、（２）、（３）より不適。
よって、b＋c＝d。

・Hamayanさん、有無相生さん、M.Hossieさん
四角形ＡＢＣＤが同一円周上にあることから、
　トレミーの定理より、AB・CD + AC・BD＝BC・AD 、
　ac＋ab＝ad、
よって、b＋c＝d。