第２２２問の解答

---

１．問題　［平面図形］

左図のような、一辺の長さが２cmの正方形ＡＢＣＤがあります。 いま、常にその両端を正方形ＡＢＣＤの辺上におく長さ２cmの線分ＰＱがあり、この線分ＰＱを自由に動かします。 このとき、線分ＰＱの中点Ｒが動いてできる線の全長を答えてください。 ただし、円周率が必要な場合は、３．１４として計算してください。

---

２．解答例１（ふぇるまーさん、高橋道広さん、N.Nishiさん、他多数）

実際に動かしてみます。

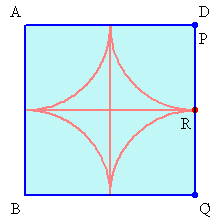
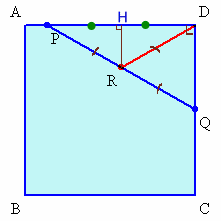
［アニメＯＮ］を押すとアニメで表示します。 　 　 ・Ｐ、Ｑが隣合う辺にあるとき： 　４分の１円×４　・・・（１） ・Ｐ、Ｑが相対する辺にあるとき 　十字形　・・・（２） となることが分かります。 よって、長さは、 　２π×１＋２×２ ＝２×３．１４＋４ ＝１０．２８ｃｍとなります。

（１）については、例えばＰがＡＤ上、ＱがＣＤ上にあるとき、

Ｄは、直角三角形ＰＱＤの外接円上にあるので、ＤＲ＝ＰＲ＝ＱＲ。
よって、ＲはＤを中心とする４分の１円の周上にある。

あるいは、ＲからＡＤに下ろした垂線の足をＨとすると、
中点連結定理により、ＡＨ＝ＤＨ。
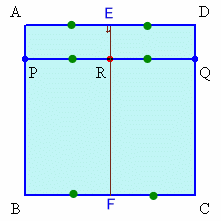
よって、△ＡＲＨ≡△ＤＥＨ、ＰＲ＝ＤＲがいえる。

（２）については、下図から明らかである。

答 １０．２８ｃｍ

　以上

---