第２２３問の解答

１．問題　［平面図形］

問題図
左の図１は、△ＡＢＣの内部に、∠ＡＰＢ＝∠ＢＰＣ＝∠ＣＰＡ（＝１２０゜）となるような点Ｐをとったところを表しており、ＰＡ＝４cm、ＰＢ＝６cm、ＰＣ＝５cmとなっています。

図２は、内部の点Ｑと各頂点を結んでできるＱＤ、ＱＥ、ＱＦの長さがそれぞれ図１の辺ＡＢ、辺ＢＣ、辺ＣＡと等しくなっている正三角形ＤＥＦを表しています。

このとき、△ＤＥＦの面積は、△ＡＢＣの何倍でしょうか。

　

２．解答例１（萬田銀次郎さん、たこやき大学さん、長野美光さん、あすとさん、ありっちさん、ヒデー王子さん、エウロパさん、あやのりんさん、中村明海さん、M.Hossieさん、井合宗太郎さん、トトロ＠Ｎさん、圭太さん、ふぇるまーさん、他多数）

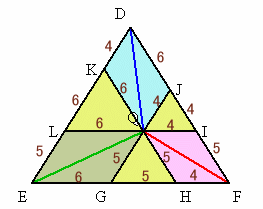
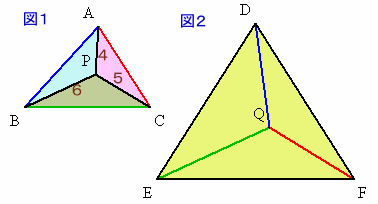
図１の△ＡＰＢ、△ＢＰＣ、△ＣＰＡをそれぞれ２つずつ合わせて平行四辺形をつくり、下図のように並べます。

参考図1

すると、正三角形ＤＥＦの１辺は１５ｃｍで、残った部分が１辺４ｃｍ、５ｃｍ、６ｃｍの３つの正三角形となります。

よって、△ＤＥＦ：△ＡＢＣ
　　＝１５2：｛１５2−（４2＋５2＋６2）｝／２
　　＝２２５：７４。

答：２２５：７４

他に、座標、三角関数、余弦定理等を用いて解いた方は、

  • すうぱあさん、Gouさん、ταροさん、ハラギャーテイさん、清川育男さん、LIONさん、有無相生さん

などでした。