第２２４問の解答

---

１．問題　［場合の数］

１から３２までの整数が書いたカードが１枚ずつ、計３２枚あります。 この計３２枚のカードの中から３枚を同時に取り出すとき、互いの数の差が２以上になるような取り出し方 は何通りあるでしょうか。

---

２．解答例１（ヒデー王子さん、高橋道広さん、noetherさん、他）

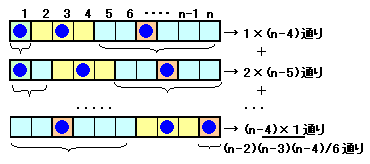
　・カード枚数がｎで、差が２以上の場合・・・（Ａ）
　・カード枚数がｎ−２で、差が２以上でなくても良い場合・・・（Ｂ）
の２通りの取り出し方を考えます。

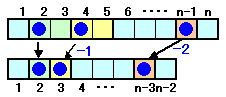
（Ａ）で取り出したときの数字を小さい順にａ、ｂ、ｃとします。
このとき、ａ、ｂ−１、ｃ−２はａ＜ｂ−１＜ｃ−２となるので、（Ｂ）の場合の１つの取り出し方になります。

逆に、（Ｂ）で取り出したときの数字を小さい順にｘ、ｙ、ｚとします。
このとき、ｘ、ｙ＋１、ｚ＋２は差が２以上あるので（Ａ）の場合の１つの取り出し方になります。

以上から、（Ａ）と（Ｂ）の取り出し方の数は等しいことになります。
（Ｂ）では、
_ｎ−２Ｃ_３＝（ｎ−２）（ｎ−３）（ｎ−４）／３・２・１
　　　　　　＝３０・２９・２８／６＝４０６０通り。

従って、（Ａ）も４０６０通りになります。

答：４０６０通り

---

３．解答例２（ふぇるまーさん、H.Takaiさん、すうぱあさん、M.Hossieさん、N.Nishiさん、せんださん、mhayashiさん、他多数）

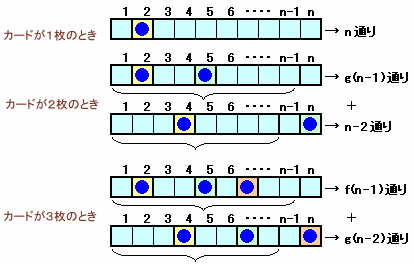
ｎ個のカードから３枚選ぶ組み合わせの数は、_nＣ₃で得られます。

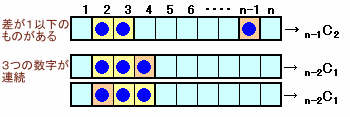
この中には、選んだカードの数字の差が１以下の場合がありますので、これを除くことにします。

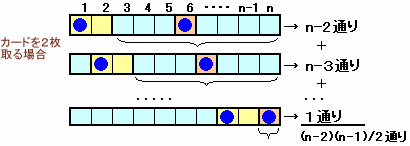
差が１以下のものがあるときは、数字が連続した２枚のカードを１組と、それ以外の１枚のカードを選ぶことになります。

これは、ｎ−１個のものから２個選ぶことと同じになりますが、選んだ２個を入れ替えたものは異なる場合になりますので、組み合わせの数は２×_n-1C₂になります。

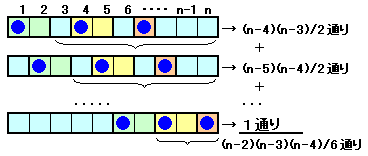
この中には、３枚連続したカードを選ぶことが含まれますが、２個のものと１個のものを入れ替えたもので重複して数えることになりますので、今度はこの分、すなわちｎ−２個のものから１個選ぶ_n-2C₁にだけ加える必要があります。

従って、求める場合の数は、
　　_nＣ₃−２×_n-1C₂＋_n-2C₁
　＝ｎ（ｎ−１）（ｎ−２）／６−２（ｎ−１）（ｎ−２）／２＋（ｎ−２）
　＝（ｎ−２）（ｎ−３）（ｎ−４）／６
　＝３０・２９・２８／６
　＝４０６０通り
となります。

４．解答例３（Gouさん、AUさん、圭太さん、あんみつさん、糸瀬善人さん、他多数）

（カードを２枚選ぶ場合）
まず、ｎ枚のカードから２枚選んで差が２以上の場合の数を求めます。

最初に選ぶカードの数字で分類します。

１のとき：隣の２は選べませんから、残りは３〜ｎまでのｎ−２通り。
２のとき：隣の３は選べませんから、残りは４〜ｎまでのｎ−３通り。
　　・・・
ｎ−２のとき：隣のｎ−１は選べませんから、残りはｎの１通り。

従ってこれらを合計すると、
　１＋２＋・・・（ｎ−２）＝（ｎ−２）（ｎ−１）／２通り
になります。

（カードを３枚選ぶ場合）
同様に、最初に選ぶカードの数字で分類します。

１のとき：残りは３〜ｎまでのｎ−４枚から２枚選ぶ（ｎ−４）（ｎ−３）／２通り。
２のとき：残りは４〜ｎまでのｎ−５枚から２枚選ぶ（ｎ−５）（ｎ−４）／２通り。
　　・・・
ｎ−４のとき：残りはｎ−２〜ｎまでの３枚から２枚選ぶ２・１／２＝１通り。

Ｓ_ｎ＝ｎ（ｎ＋１）（ｎ＋２）／３とすると、
Ｓ_ｋ−Ｓ_ｋ-1
　＝ｋ（ｋ＋１）（ｋ＋２）／３−（ｋ−１）ｋ（ｋ＋１）／３
　＝ｋ（ｋ＋１）

よって、
Σ_(k=1..n)ｋ（ｋ＋１）
　　＝Σ_(k=1..n)（Ｓ_ｋ−Ｓ_ｋ-1）
　　＝Ｓ_ｎ−Ｓ_０
　　＝Ｓ_ｎ＝ｎ（ｎ＋１）（ｎ＋２）／３　・・・（１）

求める場合の数は、
　１／２・Ｓ_ｎ−４
　＝（ｎ−４）（ｎ−３）（ｎ−２）／６　
　＝３０・２９・２８／６
　＝４０６０通り

４．解答例３（POIさん、うっしーさん、他）

真ん中のカードを最初に選ぶ方法で分類します。

３のとき：左側のカードは１のみの１通り、右側は５〜ｎまでのｎ−４通り。
４のとき：左側のカードは１〜２の２通り、右側は６〜ｎまでのｎ−５通り。
　　・・・
ｎ−２のとき：左側のカードは１〜ｎ−４のｎ−４通り、
　　右側はｎのみの１通り。

よって合計は、
　　Σ_(k=1..n-4)ｋ（ｎ−３−ｋ）
　＝（ｎ−３）Σ_(k=1..n-4)ｋ−Σ_(k=1..n-4)ｋ²
　＝（ｎ−３）（ｎ−４）（ｎ−３）／２−（ｎ−４）（ｎ−３）（２ｎ−７）／６
　＝｛（ｎ−４）（ｎ−３）／６｝｛３（ｎ−３）−（２ｎ−７）｝
　＝（ｎ−４）（ｎ−３）（ｎ−２）／６
　＝４０６０通り

５．解答例４(DrKさん、他)

漸化式で考えます。
カードｎ枚から３枚選ぶときの場合の数をｆ（ｎ）、２枚選ぶ時をｇ（ｎ）、１枚選ぶ時をｈ（ｎ）とします。

（１）カード１枚を選ぶとき：ｈ（ｎ）＝ｎ通りとなります。

（２）カード２枚を選ぶとき：

• １〜ｎ−１までのカードから２枚選ぶとき：ｇ（ｎ−１）通り

• １〜ｎ−２までのカードから１枚、およびｎのカードを選ぶとき：
  　ｈ（ｎ−２）＝ｎ−２通り

　よって、ｇ（ｎ）＝ｇ（ｎ−１）＋ｎ−２が成り立ちます。
　従って、
　　ｇ（ｎ）＝Σ_(k=1..n)（ｋ−２）＋ｇ（０）
　　　　＝（ｎ−２）（ｎ−１）／２通り
　となります。

（３）カード３枚を選ぶとき：

• １〜ｎ−１までのカードから３枚選ぶとき：ｆ（ｎ−１）通り

• １〜ｎ−２までのカードから２枚、およびｎのカードを選ぶとき：
  　ｇ（ｎ−２）＝ｎ−２通り

　よって、ｆ（ｎ）＝ｆ（ｎ−１）＋ｇ（ｎ−２）が成り立ちます。
　従って、
　　ｆ（ｎ）＝Σ_(k=1..n)（ｋ−４）（ｋ−３）／２＋ｆ（０）
　　　　＝（ｎ−４）（ｎ−３）（ｎ−２）／６　　・・・（１）より
　　　　＝４０６０通り
　となります。