第226問の解答
1.問題 [場合の数]
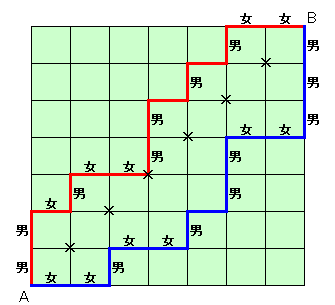
| 男子生徒が7人、女子生徒が7人います。 いま、この14人の生徒を横1列に並べます。このとき、その列のどこで区切っても、区切られた左右の両グループ内での男女の数が異なるような並び方は何通りあるでしょうか。 例えば、7人の男子生徒と、7人の女子生徒がいるとして、 女 女 男 女 女 男 女 男 男 女 女 男 男 男 ・・・・例1 のように並ぶと、どこで区切っても左右に出来たグループにおける男女数が異なるので、上の条件に当てはまります。 男 男 女 男 女 女|男 男 女 男 女 男 女 女 ・・・・例2 のように並ぶと、図の|で区切ると左のグループ(男子3人、女子3人)も右のグループ(男子4人、女子4人)も男女数が等しくなってしまいますから、当てはまりません。 (注)・・・それぞれの“人”は区別しないものとします。 |
2.解答例1(ταροさん、POIさん、みずなぎさん、長野美光さん、高橋道広さん、ありっちさん、他多数)
下図のような7×7の格子図を考えます。
AからBへ至る最短経路について、
上へ進む←→男、 右へ進む←→女
のように対応させると、7人づつの男女を並べる方法と1対1に対応します。最短経路のうち、
どこで区切っても左右に出来たグループにおける男女数が異なる:
A、B間の対角線上にある格子点を通らない ・・・・ タイプ1
どこかで区切ると左右に出来たグループにおける男女数が等しい:
A、B間の対角線上にある格子点を通る ・・・・ タイプ2に分けられるので、求める場合の数はタイプ1の最短経路の個数を数えればよいことになります。
そのため、
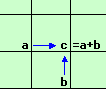
・スタート地点Aでは1とおき
・各格子では、そこに至る格子上の数字を加える(図1)
ように、次々と計算していきます。
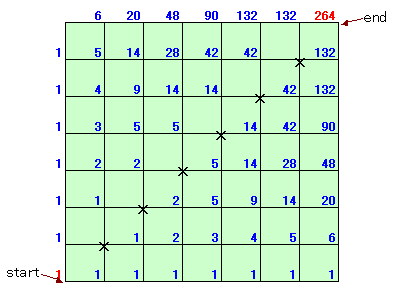
最後に求まる終点B上の数字が最短経路の個数となります。
図1
図2
本問では、図2のように計算されるので、求める場合の数は、264通りとなります。
答:264通り
3.解答例2(ヒデー王子さん、たなかさん、杉本未来さん、たこやき大学さん、萬田銀次郎さん、AЯCさん、むらかみさん、清川育男さん、他多数)
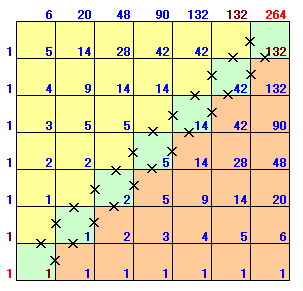
解答例1の図1は、下図のように2つの部分に分かれます。
これらはカタラン数と呼ばれます。
n次のカタラン数の一般式は、2nCn/(n+1)で求められますので、
本文の答は、
6次のカタラン数の2倍
=12C6/7×2
=132×2
=264通り
となります。