第２２７問の解答

---

１．問題　［平面図形］

左図のような、∠Ａ＝４５度の△ＡＢＣがあります。 いま、ＡからＢＣに垂線ＡＨを、ＣからＡＢに垂線ＣＩをおろし、その交点をＰとしたところ、ＢＨ＝４cm、ＣＨ＝５cmとなりました。 このとき、△ＡＰＣの面積を求めてください。

---

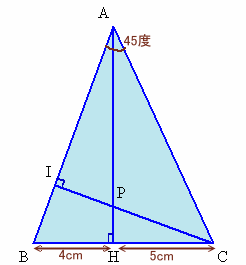２．解答例１（萬田銀次郎さん、たこやき大学さん、トトロ＠Ｎさん、C-Dさん、高松さん、高橋道広さん、ταροさん、ハラギャーテイさん、他多数）

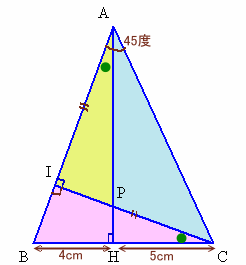
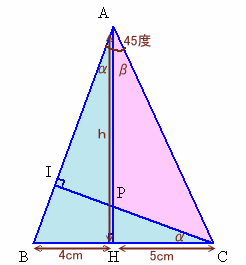
△ＡＰＩと△ＣＢＩについて考えます。

∠ＰＡＩ＝∠ＢＣＩ＝９０度−∠ＡＢＣ、
∠ＡＩＰ＝∠ＣＩＢ＝９０度、
ＡＩ＝ＣＩ（△ＡＩＣは直角二等辺三角形）
より、△ＡＰＩ≡△ＣＢＩ。

よって、ＡＰ＝ＣＢ＝９ｃｍ。

　　△ＡＰＣ
　＝1/2×ＡＰ×ＨＣ
　＝1/2×９×５
　＝４５／２ｃｍ²
となります。

答：４５／２cm²

---

３．解答例２（うっしーさん、きょえぴさん、糸瀬善人さん、みずなぎさん、他）

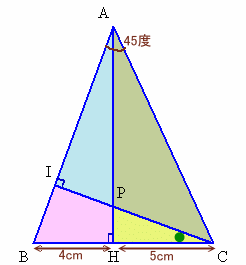
△ＣＰＨと△ＣＢＩについて考えます。

∠ＰＣＨ＝∠ＢＣＩ、∠ＣＨＰ＝∠ＣＩＢ＝９０度より、
△ＣＰＨ∽△ＣＢＩ。

ＣＩ：ＣＢ＝ＣＨ：ＣＰ、
よって、ＣＩ×ＣＰ＝ＣＨ×ＣＢ＝５×９＝４５。

　　△ＡＰＣ
　＝1/2×ＡＩ×ＣＰ
　＝1/2×ＣＩ×ＣＰ
　＝1/2×４５
　＝４５／２ｃｍ²
となります。

他の解答例として、
・ピタゴラスの定理、２次方程式、余弦定理、三角関数等を駆使して求める：
　ありっちさん、noetherさん、mhayashiさん、ハラギャーテイさん、有無相生さん、M.Hossieさん
がありました。

　（参考）三角関数を用いる解法

∠ＢＡＨ＝α、∠ＣＡＨ＝β、ＡＨ＝ｈとします。

α＋β＝４５度より、ｔａｎ（α＋β）＝ｔａｎ４５＝１。
タンジェントの加法定理より、
　ｔａｎ（α＋β）
＝（ｔａｎα＋ｔａｎβ）／（１−ｔａｎα・ｔａｎβ）
＝（４／ｈ＋５／ｈ）／（１−４／ｈ・５／ｈ）
＝１

よって、
　９／ｈ＝１−２０／ｈ²、
　ｈ²−２０＝９ｈ、　　　・・・　（１）
　ｈ²−９ｈ−２０＝０。　・・・　（２）

（２）より、ｈ＝（９＋√１６１）／２を得ます。

ＡＰ＝ＡＨ−ＰＨ
　　＝ｈ−５ｔａｎα
　　＝ｈ−５・４／ｈ
　　＝（ｈ²−２０）／ｈ
　　＝９　（（１）より）

よって、
　　△ＡＰＣ
　＝1/2×ＡＰ×ＨＣ
　＝1/2×９×５
　＝４５／２ｃｍ²
となります。