第２２８問の解答

１．問題　［整数の性質］

問題図
左図のような、１〜３６の番号の書かれた３６個の玉で出来た首飾りがあります。
この首飾りから、まず１番の玉を、その後はｐ番ごとに玉を取り外していき、その場所に玉がなかったらそこで終了とします。
また、途中で３６を越えてしまった場合には、その数から３６を引いた番号の玉を取り出し、その後同じように続けます。

例えば、ｐ＝１０の場合に取り出す玉は、
　１番→１１番→２１番→３１番→５番→１５番→２５番→３５番→９番→１９番→２９番　→３番→１３番→２３番→３３番→７番→１７番→２７番→１番
のようになりますね。

このとき、全ての玉がなくなってしまうようなｐを全て求めてください。
ただし、ｐは３６以下の整数とします。

２．解答例１（ταροさん、澪桜葵美翔さん、萬田銀次郎さん、ありっちさん、noetherさん、Gouさん、きょえぴさん、柚奇神太郎さん、香川仁志さん、高橋道広さん、すなさん、DrKさん、清川育男さん、他多数）

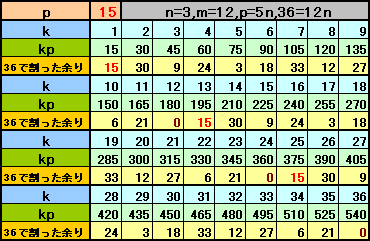
全ての玉がなくなるとは、ｐ、２ｐ、３ｐ、・・・、３６ｐのそれぞれを３６で割った余りが全て異なることを意味します。
これは、ｐが３６と互いに素のときに限ることを、次のように示すことができます。

もし、ｐと３６が公約数ｎ（ｎ＞１）を持つと仮定します。
ｐ＝ｑｎ、３６＝ｍｎ（１＜ｑ、ｍ＜３６）とかけるので、
ｍｐ＝ｍｑｎ＝３６ｑは３６の倍数となります。
（ｍ＋１）ｐ−ｐ＝ｍｐですから、ｐと（ｍ＋１）ｐは３６で割った余りが等しくなり、しかも、１＜ｍ＋１≦３６なので、ｐ、２ｐ、３ｐ、・・・、３６ｐの中に３６で割った余りが等しいものがあることになります

（例）ｐ＝１５の場合
参考図1

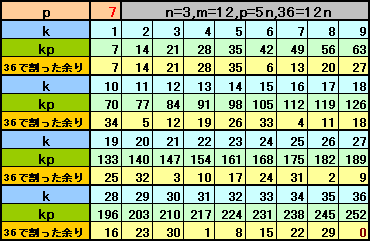
逆に、ｐと３６は互いに素とします。
もし、ｐ、２ｐ、３ｐ、・・・、３６ｐの中に余りが等しいものｎｐ、ｍｐがあったとします。（１＜ｎ＜ｍ＜３６）
ｍｐ−ｎｐ＝（ｍ−ｎ）ｐ＝３６ｋとなりますが、ｐは３６の約数を持たないので、（ｍ−ｎ）が３６の倍数となります。これは、１＜ｎ＜ｍ＜３６に反します。
従って、ｐ、２ｐ、３ｐ、・・・、３６ｐは、３６で割った余りが全て異なります。

（例）ｐ＝７の場合
参考図2

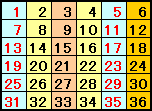
さて、３６＝２2・３2と素因数分解できるので、１、２、３、・・・、３６の中で３６と互いに素なものは、２の倍数でも３の倍数でもないものとなります。

従って、求める解は、下表の１の列、５の列の１２個となります。

　参考図3


答：１、５、７、１１、１３、１７、１９、２３、２５、２９、３１、３５