第２３０問の解答

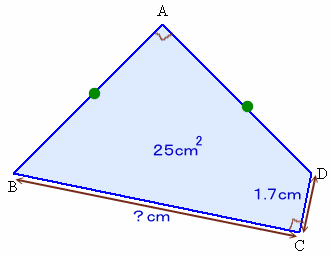
１．問題　［平面図形］

問題図
左図のような、ＡＢ＝ＡＤ、∠ＢＡＤ＝∠ＢＣＤ＝９０度の四角形ＡＢＣＤがあります。

ＤＣ＝１.７cm、四角形ＡＢＣＤの面積が２５cm2であるとするとき、ＢＣの長さは何cmでしょうか？。

２．解答例１（C-Dさん、トトロ＠Ｎさん、高橋道広さん、糸瀬善人さん、中学への算数学コンさん、他多数）

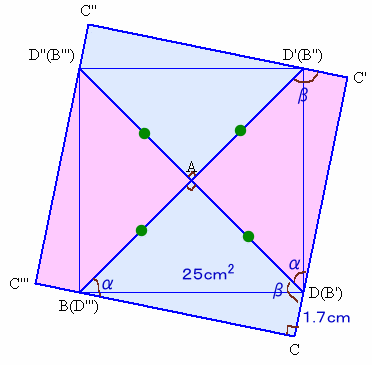
四角形ＡＢＣＤと同じ図形を４個、下図のように合わせます。

参考図1

四角形の内角の和は３６０度ですから、
　α＋β＋９０＋９０＝３６０度
よって、α＋β＝１８０度。

従って、Ｃ'、Ｄ、Ｃは一直線上に並びます。
他辺も同様ですから、ＣＣ'Ｃ''Ｃ'''は正方形になります。

この正方形の面積は、２５×４＝１００ｃｍ2ですから、１辺の長さは１０ｃｍ。
従って、ＢＣ＝Ｃ'Ｄ＝１０−１.７＝８.３ｃｍとなります。

　答：８.３ｃｍ

以上

３．解答例２（たこやき大学さん、ταροさん、澪桜葵美翔さん、ふぇるまーさん、ハラギャーテイさん、有無相生さん、M.Hossieさん、他多数）

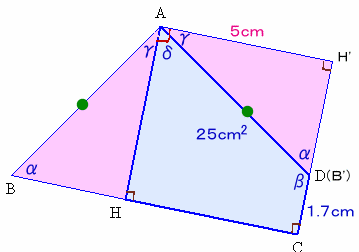
ＡからＢＣに下ろした垂線の足をＨとします。
△ＡＢＨを切り取って、ＡＢとＡＤが重なるように合わせます。

参考図2

α＋β＝１８０度より、Ｃ、Ｄ、Ｈ'は１直線上にならびます。

また、γ＋δ＝９０度より、四角形ＡＨＣＨ'の４つの角は全て直角となるので、ＡＨＣＨ'は正方形です。

この面積が２５ｃｍ2ですから、１辺の長さは５ｃｍ。
ＢＨ＝ＤＨ'＝５−１.７＝３.３ｃｍ、ＨＣ＝５ｃｍ。

よって、ＢＣ＝ＢＨ＋ＨＣ＝３.３＋５＝８.３ｃｍとなります。

　

４．解答例３（ヒデー王子さん、みずなぎさん、みもむさん、ありっちさん、うっしーさん、他多数）

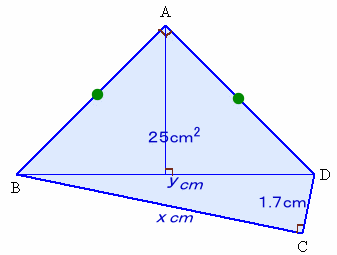
ＢＣ＝ｘｃｍ、ＢＤ＝ｙｃｍ、ＣＤ＝ａ＝１.７ｃｍとします。

参考図3

ピタゴラスの定理より、ｙ2＝ｘ2＋ａ2。

また、四角形ＡＢＣＤの面積は、
　1/4ｙ2＋1/2ａｘ＝1/4（ｘ2＋ａ2）＋1/2ａｘ＝1/4（ｘ＋ａ）2＝２５ｃｍ2。

よって、ｘ＋ａ＝１０、ｘ＝１０−ａ＝１０−１.７＝８.３ｃｍとなります。