第２３１問の解答

１．問題　［空間図形］

問題図
左図のような、立体（７面体）ＡＢＣＤＥＦがあります。
この立体は、底面ＡＢＣＤが一辺８cmの正方形となっていて、ＥＡ、ＦＣはともに６cmで底面に垂直に立っています。

いま、この立体に対して、
  • ３点Ｐ、Ｑ、Ｒを通る平面で切断
  • ３点Ｐ、Ｓ、Ｔを通る平面で切断

　という作業を行います。このとき、頂点Ｂを含む立体の体積を求めてください。ただし、Ｐは辺ＥＦの、Ｑは辺ＥＤの、Ｒは辺ＥＢの、Ｓは辺ＦＤの、Ｔは辺ＦＢの中点になっています。 

２．解答例１（C-Dさん、ヒデー王子さん、トトロ＠Ｎさん、長野美光さん、YokoyaMacさん、高橋道広さん、中村明海さん、ジン ハジメさん、ＡЯＯＴさん、あやのりんさん、糸瀬善人さん、他多数）

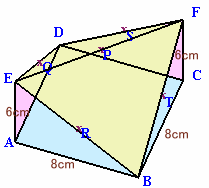
点Ｐ、Ｑ、Ｒ、Ｓ、Ｔから底面に下ろした垂線の足をＰ'、Ｑ'、Ｒ'、Ｓ'、Ｔ'、
およびＰＲ、ＰＴ、ＰＳ、ＰＱの延長線と底面の交点をＧ、Ｈ、Ｉ、Ｊとします。

図１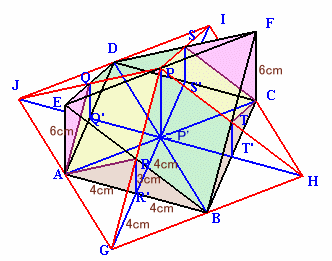
参考図1		 図２
参考図2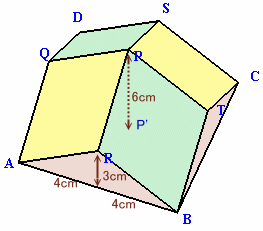

ＥＡとＲＲ'は平行でＲはＥＢの中点だから、中点連結定理よりＲ'はＡＢの中点で、ＲＲ'＝ＥＡ×1/2＝３ｃｍ。

また、ＰＰ'とＲＲ'は平行でＰＰ'：ＲＲ'＝６：３＝２：１だから、Ｒ'はＰ'Ｇの中点となり、ＧＰ'＝８ｃｍとなります。

同様に、Ｐ'Ｈ＝Ｐ'Ｉ＝Ｐ'Ｊ＝８ｃｍで、しかもこれらは互いに直交しているので、ＪＡＧ、ＧＢＨ、ＨＣＩ、ＩＤＪはそれぞれ一直線上にあります。
また、四角形ＧＨＩＪは正方形となります。

従って、Ｐ、Ｑ、Ｒを通る平面はＡを含み、Ｐ、Ｓ、Ｔを通る平面はＣを含むことが分かります。

よって、切断後の立体は図２のようになります。 

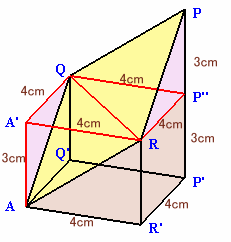
さて、この立体を４等分てできる立体の１つＡＲ'Ｐ'Ｑ'−ＲＰＱは、底面が１辺４ｃｍの正方形で、ＱＱ'＝ＲＲ'＝３ｃｍ、ＰＰ'＝６ｃｍとなります。

これを高さ３ｃｍの平面で２つに切断してできる上側の三角錐ＰＱＲＰ''は、三角錐Ａ'ＱＲＡと合同になりますから、下側の立体ににくっつけるとちょうど高さ３ｃｍの直方体になります。

参考図3

よって、求める立体の体積は、底面が正方形ＡＢＣＤで高さ３ｃｍの直方体の体積に等しくなり、８×８×３＝１９２ｃｍ3となります。

　

　答：１９２ｃｍ3

以上

３．解答例２（ありっちさん、うっしーさん、BossFさん、他多数）

参考図4

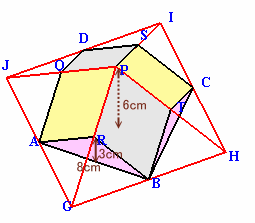
上図のように、求める立体は、四角錐Ｐ−ＧＨＩＪから４隅の三角錐を除いたものになります。

正方形ＧＨＩＪの面積は、正方形ＡＢＣＤの面積の２倍
　＝８×８×２＝１２８ｃｍ2。
よって、四角錐Ｐ−ＧＨＩＪの体積＝1/3×１２８×６＝２５６ｃｍ3。

また、三角形ＡＢＧの面積は、正方形ＡＢＣＤの面積の1/4
　＝８×８×1/4＝１６ｃｍ2。
よって、三角錐Ｒ−ＡＧＢの体積＝1/3×１６×３＝１６ｃｍ3。

従って、求める体積＝２５６−１６×４＝１９２ｃｍ3。

４．解答例３（香川　仁志さん、萬田銀次郎さん、他）

参考図5

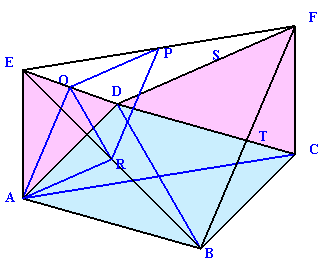
７面体ＡＢＣＤＥＦは、ＡＢＣＤを底辺とし高さ６ｃｍの直方体（体積をＶとする）から、底辺がＡＢＣＤの半分の２等辺直角三角形で高さ６ｃｍの三角錐を２個除いたものとなります。

従って、７面体ＡＢＣＤＥＦの体積＝Ｖ−1/3×1/2×Ｖ×２＝2/3×Ｖ。

三角錐ＥＡＢＤおよび三角錐ＦＣＢＤも、底辺がＡＢＣＤの半分の２等辺直角三角形で高さ６ｃｍの三角錐だから体積はそれぞれ1/6×Ｖ。

よって、四面体ＥＢＦＤの体積は、2/3×Ｖ−1/6×Ｖ×２＝1/3×Ｖ。

四面体ＥＰＱＲと四面体ＥＢＦＤは相似で相似比は１：２。
よって、四面体ＥＰＱＲの体積は1/3×Ｖ×1/8＝1/24×Ｖ。

従って、求める体積＝2/3×Ｖ−1/24×Ｖ×４
　＝1/2×Ｖ＝1/2×８×８×６＝１９２ｃｍ3。