第２３２問の解答

１．問題　［規則性］

０〜１３の整数が書かれたカードが１枚ずつ、合計１４枚あります。その中から、次の条件に合うようにしながらできるだけ多くのカードを取り出すことを考えます。

条件：「取り出されたカードの中から３枚のカードを選び出して小さい順に並べる。このとき、どんな取り出し方をしても隣どうしの数の差が等しくならない。」

この場合は、０、１、３、４、９、１０、１２、１３の書かれたカードを取り出せば、上の条件に合いますね。

では、０〜１２１の整数が書かれたカードが１枚ずつ、合計１２２枚あります。その中から上の条件に合うようにできるだけ多くのカードを取りだすとすると、全部で何枚のカードを取り出すことができるでしょうか。

２．解答例１（長野美光さん、Gouさん、ありっちさん、ταροさん、AUさん、うっしーさん、高橋道広さん、トトロ＠Ｎさん、糸瀬善人さん、ふぇるまーさん、ハラギャーテイさん、有無相生さん、M.Hossieさん、H.Takaiさん、他多数）

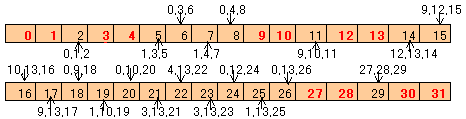
０、１からはじめて、条件に合うカードナンバーを下図のように次々と求めていきます。（図では条件に合わない場合の３枚のカードを補足しています。）

図１
参考図1

すると、下図のとおりになります。

図２
参考図2

従って、０から１２１までのカードからは、
0、1、3、4、9、10、12、13、27、28、30、31、36、37、39、40、
81、82、84、85、90、91、93、94、108、109、111、112、117、118、120、121
の３２枚が条件を満たすことが分かります。

なお、条件に合うカード番号を見つけていくときに、カード番号の差の規則性に注目していけば、比較的容易に求まります。
（ただし、何人かの方が対象性に言及していますが、３３枚目の４１、４９枚目の１２２など必ずしも対象性に当てはまらないものがあります。）

　答：３２枚

以上

３．解答例２（ジン ハジメさん、長野美光さん、BossFさん、中学への算数学コンさん、ヘロン久野さん、清川育男さん、げんさん、他多数）

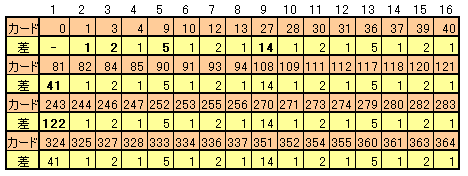
解答例１で求まった３２枚のカード番号を３進数で置き換えてみると、
0、1、10、11、100、101、110、111、1000、1001、1010、1011、1100、1101、1110、1111、　10000、10001、10010、10011、10100、10101、10110、10111、11000、11001、11010、11011、11100、11101、11110、11111
のように、２の数字を使わないものが並びます。

これらを、２進数とみなすと、０から１１１１１（１０進数では０から３１）の３２通りあることが分かります。

　

さて、これらから任意の３つの番号を選んだとき、隣り合う数字の差が等しくならないことは次のようにして分かります。

３つの数字を小さい順にａ、ｂ、ｃとすると、隣り合う数字の差が等しくなるのは、ｂ−ａ＝ｃ−ｂ、すなわちａ＋ｃ＝２ｂ。

ところが、ｂの各桁の数字は、０また１ですから２倍すると、０または２で、桁上がりはありません。（例えば、ｂ＝１０１０のとき、２ｂ＝２０２０）

従って、２ｂの各桁について、
　２ｂの桁が０のとき：ａ、ｃの同じ桁も０
　２ｂの桁が２のとき：ａ、ｃの同じ桁は１
でなくてはなりません。
ところがこれはａ＝ｃ（上記例では、ａ＝ｃ＝１０１０）を意味しますので、不適です。

よって、ａ＋ｃ＝２ｂとなることはあり得ません。

　

次に、２の数字が含まれる任意のｃに対しては、ａ＋ｃ＝２ｂとなるａ、ｂ（２を含まない番号）が必ず１組は存在することが次のようにして分かります。

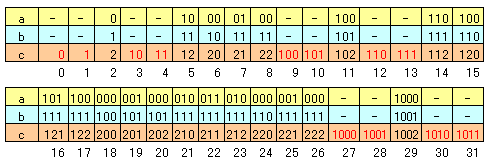
ｃ＝ｃnｃn-1・・・ｃ1ｃ0に対して、ａ＝ａnａn-1・・・ａ1ａ0、ｂ＝ｂnｂn-1・・・ｂ1ｂ0を次のように定めます。（図３参照）
　ｃk＝０のとき：ａk＝０、ｂk＝０
　ｃk＝１のとき：ａk＝１、ｂk＝１
　ｃk＝２のとき：ａk＝０、ｂk＝１
（例えば、ｃ＝１２１に対して、ａ＝１０１、ｂ＝１１１）

図３
参考図3

このとき、ｐ＝ａ＋ｃ、ｑ＝２ｂの各桁は、
　ｃk＝０のとき：ａk＝０、ｂk＝０より、ｐk＝０、ｑk＝０
　ｃk＝１のとき：ａk＝１、ｂk＝１より、ｐk＝２、ｑk＝２
　ｃk＝２のとき：ａk＝０、ｂk＝１より、ｐk＝２、ｑk＝２
となり、ａ＋ｃ＝２ｂが成り立つことが分かります。
（例えば、ｃ＝１２１に対して、ａ＝１０１、ｂ＝１１１、ａ＋ｃ＝２２２、２ｂ＝２２２）

しかも、ａおよびｂは、ｃより必ず小さくてかつ２を含まない番号となるので、
最初の２つのカード番号を０、と１から始めれば、帰納法により２を含む番号は不適であることが分かります。

（補足）本問では、解答例１、２等から必ずしも３２枚が最大であることは示せません。というのは、最初の２枚の番号が０と１以外の場合について調べていないからです。
例えば、カード番号が０から８までの場合では、 上記解法では、０、１、３、４の４枚が最大となりますが、これ以外に０、１、５、６、８という５枚のカード番号が条件を満たします。

しかしながら、げんさんによれば０から１２１までの場合、プログラムの計算により３２枚が最大であることが確認されました。