第２３３問の解答

---

１．問題　［速さの問題］

６０km離れたＡ地点、Ｂ地点があり、Ａ地点にマサルさん、Ｂ地点にトモエさんがいます。 いま、２人が同時に両地点を出発します。 マサルさんは４時間後にまずＰ地点でトモエさんに出会いました。 その後Ｂ地点に到着したマサルさんは速さを変えてＡ地点に向かって引き返し、 １回目に出会ってから１時間後にＱ地点でトモエさんを追い抜きました。 さらにその後、Ａ地点に到着したマサルさんは初めの速さに戻してＢ地に向かって引き返し、 追い越してから５時間後にＲ地点でトモエさんに出会いました。 ＡＰ間の距離は何kmでしょうか。 ＡＲ間の距離は何kmでしょうか。 ※・・・２人は上記の３回以外には出会ったり、追い抜いたりしなかったものとします。

---

２．解答例１（高橋道広さん、トトロ＠Ｎさん、ありっちさん、中村明海さん、澪桜葵美翔さん、萬田銀次郎さん、圭太さん、糸瀬善人さん、げんたさん、noetherさん、げんさん、あまれっとさん、ZIMBAさん、他多数）

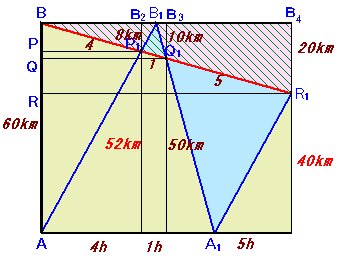
ダイアグラムで考えます。

上図で、マサルさんがＡ地点からＢ地点へ向かう速度は、最初と２度目では同じなので、ＡＢ₁とＣ₁Ｒ₁は平行、よって△Ｐ₁Ｂ₁Ｑ₁と△Ｒ₁Ｃ₁Ｑ₁は相似になります。

トモエさんは、ＰＱ間を１時間、ＱＲ間を５時間で進んだことになるので、
　ＰＱ：ＱＲ＝１：５、よって、Ｂ₁Ｑ₁：Ｑ₁Ｃ₁＝ＢＱ：ＱＡ＝１：５。
従って、
　ＢＱ＝ＡＢ×１/６＝１０km、ＡＱ＝ＡＢ×５/６＝５０km
となります。

また、△ＢＰ₁Ｂ₂と△ＢＱ₁Ｂ₃および△ＢＲ₁Ｂ₄は相似で、
相似比はＢＢ₂：Ｂ₂Ｂ₃：Ｂ₃Ｂ₄＝４：５：１０、
よって、
　ＢＰ＝Ｂ₂Ｐ₁＝Ｂ₃Ｑ₁×４／５＝１０×４／５＝８km、
　ＡＰ＝６０−８＝５２km、
　ＢＲ＝Ｂ₄Ｒ₁＝Ｂ₃Ｑ₁×１０／５＝１０×１０／５＝２０km、
　ＡＲ＝６０−２０＝４０km
となります。

　答：（１）５２ｋｍ　（２）４０ｋｍ

以上

---

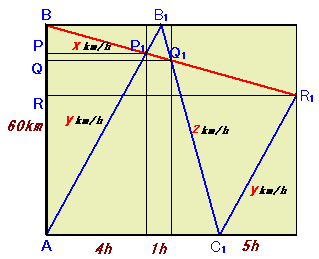
３．解答例２（はまやさん、ハラギャーテイさん、M.Hossieさん、うっしーさん、清川育男さん、水宮英理さん、他多数）

トモエさんの速さをｘkm/h、マサルさんのＡＢ間の速さをｙkm/h、ＢＡ間のｚkm/hとします。

出発して４時間後に二人は出会いますから、
　４（ｘ＋ｙ）＝６０
よって、ｘ＋ｙ＝１５　・・・　（１）

次の１時間でマサルさんは、Ｂで折り返し、トモエさんをＱで追い越します。
マサルさんがＰからＢへ行くのに要する時間は、４ｘ／ｙ、
ＢからＱへ要する時間は、５ｘ／ｚ、
よって、４ｘ／ｙ＋５ｘ／ｚ＝１　・・・　（２）

さらに、次の５時間でマサルさんは、Ａに戻り、折り返してＲでトモエさんと出会います。
マサルさんがＱからＡへ行くのに要する時間は、（６０−５ｘ）／ｚ、
ＡからＲへ要する時間は、（６０−１０ｘ）／ｙ、
よって、（６０−５ｘ）／ｚ＋（６０−１０ｘ）／ｙ＝５　・・・　（３）

（１）より、ｙ＝１５−ｘ、
（２）、（３）に代入して、
　　４ｘ／（１５−ｘ）＋５ｘ／ｚ＝１ 　・・・　（２）'
　（６０−５ｘ）／ｚ＋（６０−１０ｘ）／（１５−ｘ）＝５ 　・・・　（３）'

（２）'、（３）'より、
　５ｘ／ｚ＝１−４ｘ／（１５−ｘ）＝（１５−５ｘ）／（１５−ｘ）　・・・　（２）''
　（６０−５ｘ）／ｚ＝５−（６０−１０ｘ）／（１５−ｘ）
　　＝（１５＋５ｘ）／（１５−ｘ）　・・・　（３）''

（２）''／（３）''より、
　ｘ／（１２−ｘ）＝（３−ｘ）／（３＋ｘ）
　ｘ（３＋ｘ）＝（１２−ｘ）（３−ｘ）
　３ｘ＋ｘ²＝３６−１５ｘ＋ｘ²
　１８ｘ＝３６
よって、ｘ＝２km/h、ｙ＝１５-２＝１３km/s。

従って、ＢＰ＝４ｘ＝８km、ＢＲ＝１０ｘ＝２０km、
よって、ＡＰ＝６０−８＝５２km、ＡＲ＝６０−２０＝４０kmとなります。

---

（その他の解法）

・ダイアグラムを座標で表して解く・・・長野美光さん

などがありました。

---