第２３４問の解答

１．問題　［場合の数、平面図形］

問題図
まるい形をした赤・青・黄・緑・紫・橙・桃の７色のセロファンがあります。

このセロファンを、白い四角形の画用紙の上に置いていきます。例えば、３枚のセロファンを置くと、左図のように（白も含めて）最大で８色ができます。

では、７枚すべてを使うと最大何色ができるでしょうか？

(注)セロファンを重ねたときに、全て異なる色になるものとします。

２．解答例１（うっしーさん、水宮英理さん、ふぇるまーさん、きょえぴさん、noetherさん、N.Nishiさん、糸瀬善人さん、他多数）

セロファンの枚数をｎとして、ｎ＝１〜４の場合を描いてみます。
（図の色付けは、領域数を数えやすくしています）

参考図1

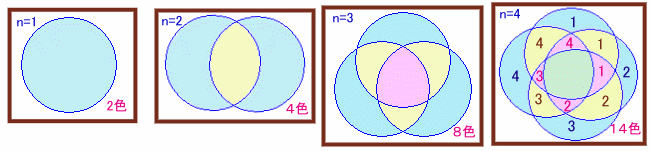
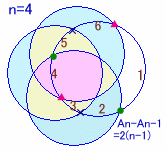
最大色数をAnとすると、一見An＝２nで表されそうですが、
ｎ＝４のときA4＝１４となりますので、どうも違うようです。

参考図2

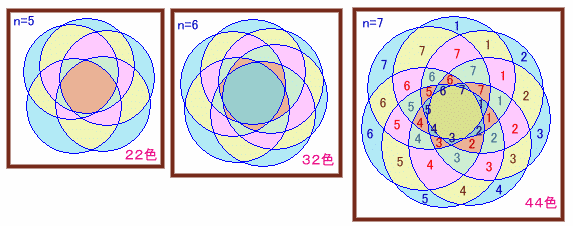
さらに、ｎ＝５〜７の場合を描いてみると、

  • セロファンが１枚も重ならない場合・・・１色

  • 　　〃　　　　１枚の場合　　　　　　・・・　ｎ色

  • 　　〃　　　　２枚重なる場合　　　・・・　ｎ色
    　　・・・・

  • 　　〃　　　（ｎ−１）枚重なる場合・・・　ｎ色

  • 　　〃　　　　ｎ枚重なる場合　　　・・・　１色

となるので、An＝n(n-1)+2が成り立つようですので、
ｎ＝７の場合は、７×６＋２＝44色と予想されます。

（注）この方法では、４４色を作ることは分かりますが、
　　　　４５枚以上はできないことを示せてはいません。

　答：４４色

以上

３．解答例２（ταροさん、萬田銀次郎さん、C-Dさん、はまやさん、中村明海さん、澪桜葵美翔さん、有無相生さん、M.Hossieさん、みずなぎさん、圭太さん、他多数）

Anに関する漸化式を考えます。

参考図3 参考図4

２つの円は最大２点でしか交わらないことに注意しましょう。
(n-1)個の円でAn-1色できているところに、もう一つの円を付け加えたとき、それぞれの円との交点は高々２個ですから、最大２（ｎ−１）個の交点が増えることになります。

このとき、ｎ番目の円は２ｎ個の円弧に分割されますが、円弧１つに対し新たな領域が１個増えることになるので、An−An-1＝２（ｎ−１）となります。

A1＝２から順に計算していくと、A7＝４４を得ます。

参考図5


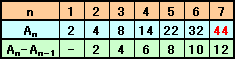
なお、Anの一般式は次のように求まります。
An＝ A1＋Σ2k (k=1..n-1)
　　＝２＋２ｎ（ｎ−１）／２
　　＝ｎ（ｎ−１）＋２

（注）この方法では、最大４４色までしか作れないことは分かりますが、
　　　　実際４４枚作れるかどうかは示せてはいません。

従って、解答例１と解答例２を合わせれば、最大４４色であることが分かります。