第２３５問の解答

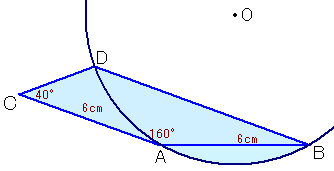
１．問題　［平面図形］

問題図
左図は、次のようにして作図されています。

１．ある円の周上に長さ６cmの弦ＡＢをとる。
２．角ＣＡＢ＝１６０度、ＣＡ＝ＡＢとなるような点Ｃをとる。
３．点Ｂから、ＡＣに平行な直線をひき、もとの円との交点をＤとする。
４．ＤとＣを結ぶ。

すると、角ＡＣＤ＝４０度となったそうです。

このとき、図の水色の部分の面積を求めてください。なお、円周率は３.１４として計算してください。

２．解答例１（ありっちさん、萬田銀次郎さん、中村明海さん、ταροさん、たこやき大学さん、うっしーさん、トトロ＠Ｎさん、C-Dさん、あやのりんさん、圭太さん、げんたさん、M.Hossieさん、あんみつさん、noetherさん、他多数）


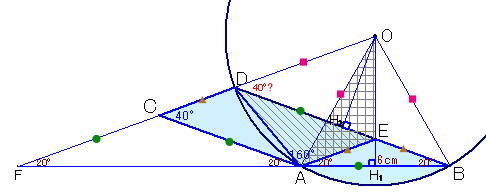
円の中心をＯとします。
中心Ｏは、辺ＡＢの垂直２等分線と辺ＢＤの垂直２等分線の交点として求まります。
図を正確に描くと、Ｃ、Ｄ、Ｏが一直線上に並んでいるようです。
これが成り立つものとして考えてみましょう。
　　（解答例２以下で、証明方法を紹介します）

参考図1

辺ＡＢの垂線２等分線ＯＨ1と辺ＢＤの交点をＥとし、辺ＢＡの延長線と辺ＤＣの延長線の交点をＦとします。

∠ＣＡＦ＝１８０−∠ＣＡＢ＝１８０−１６０＝２０度、
∠ＣＦＡ＝∠ＡＣＤ−∠ＣＡＦ＝４０−２０＝２０度。
よって、△ＣＦＡは２等辺三角形。

ＡＣとＢＤは平行より、∠ＥＢＡ＝∠ＣＡＦ＝２０度、
ＥＨ１はＡＢの垂直２等分線だから、∠ＥＡＢ＝∠ＥＢＡ＝２０度。
よって、ＡＥとＣＤは平行となり、四角形ＤＣＡＥは平行四辺形となります。

Ｃ、Ｄ、Ｏは一直線上にある（と仮定した）ので、ＯＤはＡＥと平行。
従って、△ＤＡＥと△ＯＡＥは底辺ＡＥおよび高さが共通となるので、
　△ＤＡＥ＝△ＯＡＥ。

また、四角形ＤＣＡＥは平行四辺形だから、△ＤＣＡ＝△ＤＡＥ、
ＥＨ１はＡＢの垂直２等分線だから、△ＯＢＥ＝△ＯＡＥ。

以上から、平行四辺形ＤＣＡＥの面積＝△ＯＡＥ＋△ＯＢＥ、
よって、求める図形の面積＝扇形ＯＡＢの面積。
従って、あとは円Ｏの半径と、扇形ＯＡＢの中心角ＡＯＢが分かれば面積が求まります。

参考図2

ＡＣとＢＤが平行より、∠ＯＤＢ＝∠ＤＣＡ＝４０度。
ＯＤ＝ＯＡ＝ＯＢ＝円Ｏの半径。
従って、△ＯＤＢは２等辺三角形だから、∠ＯＢＤ＝∠ＯＤＢ＝４０度、
∠ＯＢＡ＝∠ＯＢＤ＋∠ＡＢＤ＝４０＋２０＝６０度。

△ＯＡＢは２等辺三角形だから、∠ＯＡＢ＝∠ＯＢＡ＝６０度、
よって、△ＯＡＢは正三角形となり、∠ＡＯＢ＝６０度、ＯＢ＝ＡＢ＝６ｃｍと分かります。

　求める図形の面積
＝扇形ＯＡＢの面積
＝円Ｏの面積×∠ＡＯＢ／３６０
＝π×６2×６０／３６０
＝６π
≒６×３．１４
＝１８．８４ｃｍ2

　答：18.84cm2

　

以上

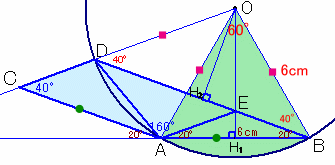
３．解答例２（noetherさん、あんみつさん、他）

辺ＣＤの延長上に、ＡＣ＝ＡＰとなる点Ｐをとります。

参考図3

△ＡＣＰは２等辺三角形となるので、∠ＡＰＣ＝∠ＡＣＰ＝４０度、
∠ＣＡＰ＝１８０−４０×２＝１００度。

よって、∠ＰＡＢ＝∠ＣＡＢ−１００＝１６０−１００＝６０度となるので、
２等辺三角形△ＰＡＢは正三角形となります。
従って、ＰＢ＝ＰＡ。　・・・（１）

また、∠ＰＢＡ＝６０度、
∠ＰＢＤ＝∠ＰＢＡ−∠ＤＢＡ＝６０−２０＝４０度。

∠ＰＤＢ＝∠ＰＢＤ＝４０度より、△ＰＤＢは２等辺三角形。
よって、ＰＤ＝ＰＢ。・・・（２）

（１）、（２）より、ＰＤ＝ＰＡ＝ＰＢ＝６ｃｍとなるので、点Ｐは円の中心となります。

以下、解答例２と同様。

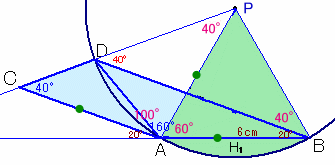
４．解答例３（M.Hossieさん、他）

ＡＢの垂直２等分線上にＡＰ＝ＢＰ＝ＡＢ＝６ｃｍとなる点Ｐをとります。

参考図4

△ＰＡＢは正三角形となるので、∠ＰＡＢ＝∠ＰＢＡ＝∠ＡＰＢ＝６０度。

∠ＣＡＰ＝∠ＣＡＢ−∠ＰＡＢ＝１６０−６０＝１００度。

ＡＣ＝ＡＰ＝６ｃｍより、△ＡＣＰは２等辺三角形、
よって∠ＰＣＡ＝９０−∠ＣＡＰ×1/2＝９０−１００×1/2＝４０度。

∠ＰＣＡ＝∠ＤＣＡ＝４０度より、Ｃ、Ｄ、Ｐは一直線上にあります。

よって、ＡＣとＢＤが平行より、∠ＰＤＢ＝∠ＰＣＡ＝４０度。

ところで、∠ＰＢＤ＝∠ＰＢＡ−∠ＤＢＡ＝６０−２０＝４０度、
よって、△ＰＤＢは２等辺三角形、ＰＤ＝ＰＢ＝６ｃｍ。

以上から、ＰＤ＝ＰＡ＝ＰＢ＝６ｃｍとなり、点Ｐは円の中心となります。

以下、省略。

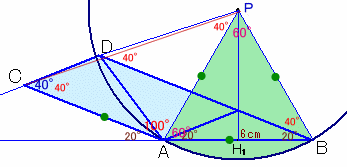
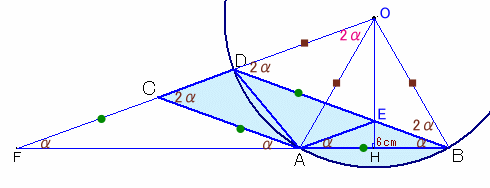
（参考）Ｃ、Ｄ、Ｏが一直線上にあるときの条件は？

この問題では、Ｃ、Ｄ、Ｏが一直線上にあることがポイントになっています。
そこで、下図のように一般化して、角度αがどうなるかを考えてみましょう。
すなわち、ＡＣとＢＤが平行、∠ＡＣＤ＝２α、∠ＣＡＢ＝１８０−αとします。（本文では、α＝２０度）

参考図5

ＨをＡＢの中点、ＥをＯＨとＢＤの交点、ＦをＢＡの延長とＤＣの延長の交点とします。
解答例１と同様に、ＡＣとＢＤが平行より、∠ＥＢＡ＝∠ＣＡＦ＝α、
△ＥＡＢは２等辺三角形より、∠ＥＡＢ＝∠ＥＢＡ＝α、
∠ＣＦＡ＝∠ＤＣＡ−∠ＣＡＦ＝２α−α＝α、
よってＡＥとＣＤが平行となることが分かります。

また、ＡＣとＢＤが平行より、∠ＯＤＢ＝∠ＯＣＡ＝２α。

Ｏは円の中心だから、ＯＤ＝ＯＡ＝ＯＢ。
よって、△ＯＤＢは２等辺三角形。
従って、∠ＯＢＤ＝∠ＯＤＢ＝２α。

また、∠ＤＯＡ（弧ＡＤの中心角）＝∠ＤＢＡ（弧ＡＤの円周角）×２＝２α。
∠ＡＣＯ＝∠ＡＯＣ＝２αより、△ＡＣＯは２等辺三角形、
よって、ＡＯ＝ＡＣ＝６ｃｍ。

従って、ＯＡ＝ＯＢ＝６ｃｍ＝ＡＢとなり、△ＯＡＢは正三角形。

よって、∠ＯＢＡ＝∠ＯＢＤ＋∠ＥＢＡ＝３α＝６０度、
従って、α＝２０度となります。

以上から、Ｃ、Ｄ、Ｏが一直線上にあるときは、α＝２０度のときに限り、
このとき、△ＯＡＢは正三角形になります。