第２３６問の解答

---

１．問題　［平面図形］

左図は、△ＡＢＣの辺ＢＣ上にＡＣ＝ＥＣとなる点Ｅをとり、さらに、∠ＢＡＥ＝∠ＥＡＤとなる点Ｄをとったところを示しています。 いま、△ＡＢＥの面積は、△ＡＥＤの面積よりも２cm2だけ大きく、△ＡＤＣの面積は１８cm2でした。 　このとき、△ＡＢＣの面積は何cm2でしょうか。

---

２．解答例１（トトロ＠Ｎさん、ありっちさん、C-Dさん、mhayashiさん、たこやき大学さん、澪桜葵美翔さん、BONZさん、あやのりんさん、M.Hossieさん、ハラギャーテイさん、他多数）

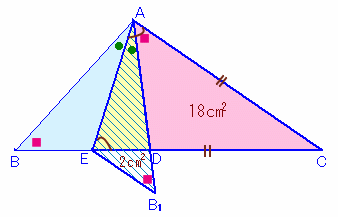
△ＡＢＥを辺ＡＥを軸にして折り返し△ＡＢ₁Ｅとします。

まず、∠ＡＢ₁Ｅ＝∠ＡＢＥが成り立ちます。　・・・（１）

∠ＡＥＣ＝∠ＡＢＥ＋∠ＢＡＥ　
∠ＥＣＡ＝∠ＥＡＤ＋∠ＤＡＣ　

△ＣＡＥは二等辺三角形だから、∠ＡＥＣ＝∠ＥＣＡ。
よって、∠ＡＢＥ＋∠ＢＡＥ＝∠ＥＡＤ＋∠ＤＡＣ。

（１）、および∠ＢＡＥ＝∠ＥＡＤより、∠ＡＢ₁Ｅ＝∠ＤＡＣ。

従って、△ＡＤＣと△Ｂ₁ＥＤは相似となります。
△ＡＤＣ＝１８ｃｍ²、△Ｂ₁ＥＤ＝△ＡＢＥ−△ＡＥＤ＝２ｃｍ²。
よって、面積比が１８：２＝９：１となり、相似比は３：１。

これから、ＣＤ：ＤＥ＝３：１が得られます。

△ＡＥＤと△ＡＤＣの高さは共通なので、面積比は底辺の長さに比例。
△ＡＥＤ：△ＡＤＣ＝ＣＤ：ＤＥ＝３：１、
△ＡＥＤ＝△ＡＤＣ×１／３＝１８×１／３＝６ｃｍ²、
△ＡＢＥ＝△ＡＥＤ＋２＝６＋２＝８ｃｍ²。

よって、△ＡＢＣ＝△ＡＢＥ＋△ＡＥＤ＋△ＡＤＣ＝８＋６＋１８＝３２ｃｍ²。

　答：３２cm²

　

以上

---

３．解答例２（はまやさん、うっしーさん、他）

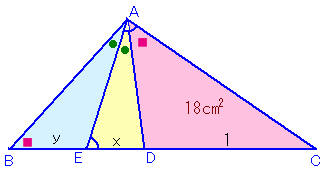
ＤＣ：ＥＤ：ＢＥ＝１：ｘ：ｙとします。

△ＡＢＥ＝１８ｙ、△ＡＥＤ＝１８ｘとなるので、１８ｙ−１８ｘ＝２、
よって、ｙ−ｘ＝１／９ｃｍ²。

解答例１と同様にして、∠ＡＢＥ＝∠ＤＡＣ。
△ＡＢＣと△ＤＣＡについて、
∠ＡＢＥ＝∠ＤＡＣ、∠ＡＣＤは共通だから△ＡＢＣと△ＤＣＡは相似。
よって、ＢＣ：ＣＡ＝ＣＡ：ＤＣ。
　（１＋ｘ＋ｙ）：（１＋ｘ）＝（１＋ｘ）：１
　１＋ｘ＋ｘ＋1/9＝（１＋ｘ）²＝１＋２ｘ＋ｘ²
　ｘ²＝1/9
よって、ｘ＝1/3、ｙ＝ｘ＋1/9＝1/3＋1/9＝4/9。

△ＡＢＥ＝１８ｙ＝１８×４／９＝８ｃｍ²、
△ＡＥＤ＝１８ｘ＝１８×１／３＝６ｃｍ²。

従って、△ＡＢＣ＝△ＡＢＥ＋△ＡＥＤ＋△ＡＤＣ＝８＋６＋１８＝３２ｃｍ²。

---

４．解答例３

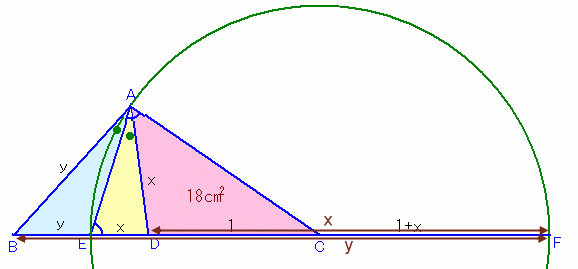
ＤＣ：ＥＤ：ＢＥ＝１：ｘ：ｙとします。
ＢＣの延長線上にＣＦ＝ＥＣとなる点Ｆをとります。

∠ＢＡＥ＝∠ＤＡＥより、△ＡＢＥ：△ＡＥＤ＝ＡＢ：ＡＤ＝ＢＥ：ＥＤ＝ｙ：ｘ。

したがって、Ａ、Ｅは、ＢおよびＤからの距離がｙ：ｘとなるアポロニウスの円の周上にある。
その中心は、直線ＢＣ上にあり、ＥＣ＝ＡＣだから、点Ｃが中心となる。

よって、点Ｆは円の直径の一端となるので、
　ＢＦ：ＤＦ＝ｙ：ｘ
　（２＋２ｘ＋ｙ）：（２＋ｘ）＝ｙ：ｘ
　２ｘ＋２ｘ²＋ｘｙ＝２ｙ＋ｘｙ
よって、ｘ＋ｘ²＝ｙ　・・・（１）

解答例２と同様にして、ｙ−ｘ＝1/9　・・・（２）

（１）、（２）より、
　ｘ＋ｘ²＝ｘ+1/9
　ｘ²＝1/9
　ｘ＝1/3

以下、省略。

---

（その他の解法）

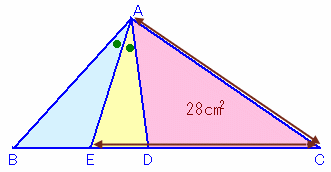
・△ABEをAがBに、BがAになるようにひっくり返してつけて、相似比で求める
　　　・・・高橋　道広さん
・△AEDをＡＥを軸に折り返して、相似比で求める
　　　・・・noetherさん、ヘロン久野さん