第237問の解答
1.問題 [速さの問題]
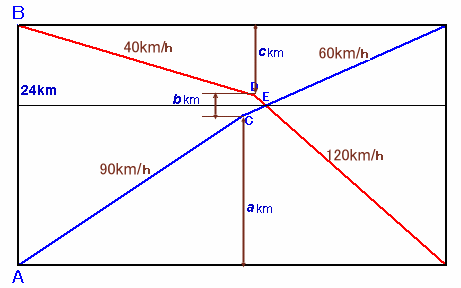
| 24km離れたA町、B町にそれぞれマサルさん、トモエさんがいます。 いま、2人はクルマで同時に出発し、マサルさんはB町に、トモエさんはA町に向かいました。 マサルさんは初め毎時90kmで走りましたが、途中のC町からは毎時60kmで走りました。 トモエさんは初め毎時40kmでしたが、途中のD町から毎時120kmで走りました。 このとき、2人のクルマはC町とD町のちょうど真ん中の地点で出会い、同時に目的地に到着したそうです。 (1) A町〜C町間の距離は何kmだったでしょうか。 (2) B町〜D町間の距離は何kmだったでしょうか。 |
2.解答例1(gappoさん、Takeさん、田村稔さん、mhayashiさん、ありっちさん、ταροさん、高橋道広さん、圭太さん、bpさん、M.Hossieさん、他多数)
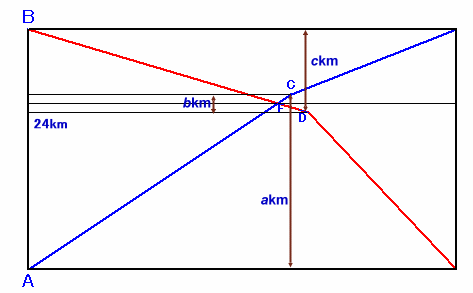
AC、CD、DB間の距離をa、b、ckm/s、とします。
出会うまでの時間は、
マサルさん ・・・ a/90 + b/2/60
トモエさん ・・・ c/40 + b/2/120
よって、
a/90 + b/2/60 = c/40 + b/2/120 ・・・(1)AB間の全所要時間は、
マサルさん ・・・ a/90 + (b+c)/60
トモエさん ・・・ c/40 + (a+b)/120
よって、
a/90 + (b+c)/60 = c/40 + (a+b)/120 ・・・(2)また、AB間の距離は、
a+b+c = 24 ・・・(3)(1)、(2)、(3)より、
a = 15、b = 2、c = 7
を得る。よって、AC間は15km、DB間は7kmと分かります。
なお、上記は、A、C、D、Bの順になっていると考えましたが、
A、D、C、Bの順になっている場合は不適であることが次のようにして分かります。
上記同様に、
(a-b/2)/90 = (c-b/2)/40 ・・・(1)'
a/90 + (c-b)/60 = c/40 + (a-b)/120 ・・・(2)'
a-b+c = 24 ・・・(3)
より、
a = 207/13, b = -18/13, c = 87/13
を得る。 これは、不適。
答: (1)15km (2)7km
以上
3.解答例2(ヒデー王子さん、げんさん、M.Hossieさん、H.Takaiさん、他)
2人が出会った地点をEとします。
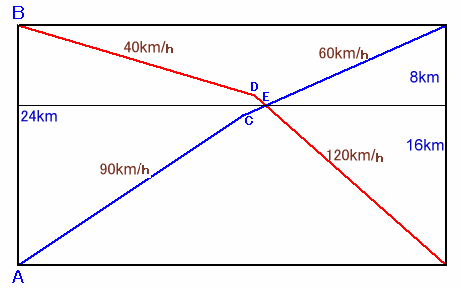
A、C、E、D、Bの順になっているとします。
E地点からマサルさんが60km/sでB地点まで行ったのとちょうど同じ時間でトモエさんはE地点からA地点まで120km/sで進んだのだから、
AE:EB=120:60=2:1
よって、AE=24×2/3=16km、EB=24×1/3=8km
となります。ダイアグラムの中央部分を拡大します。
マサルさんがAからEまで90km/hでそのまま進んだときの所要時間は、
16/90時間=16/90×60分=32/3分、
トモエさんがBからEまで40km/hでそのまま進んだときの所要時間は、
8/40時間=8/40×60分=12分、
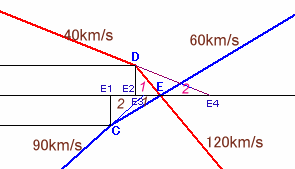
従って、その差は12−32/3=4/3分となります。マサルさんは、実際にはCEを60km/hで進んだので、所用時間の比は、60:90=2:3、よって、E1E3:E3E=2:1 ・・・(1)
トモエさんは、実際にはDEを120km/hで進んだので、所用時間の比は、120:40=3:1、よって、E2E:EE4=1:2 ・・・(2)
となります。CE=EDであり、この同じ距離をマサルさんは60km/h、トモエさんは120km/hで進んだのだから、E1E:E2E=2:1 ・・・(3)
となります。E2Eの時間を1とすると、E3E=E1E×1/3=2×1/3=2/3。
従って、E3E4=2/3+2=8/3。
この実際の時間は、4/3分だから、
E2Eの実際の時間は、(4/3分)/(8/3)=1/2分となります。よって、トモエさんはDEを120km/hで1/2分進んだのだから、
DE=60分/時間×1/2分×120km/h=1kmと分かります。よって、AC=AE−CE=16−1=15km、
DB=EB−ED=8−1=7kmとなります。
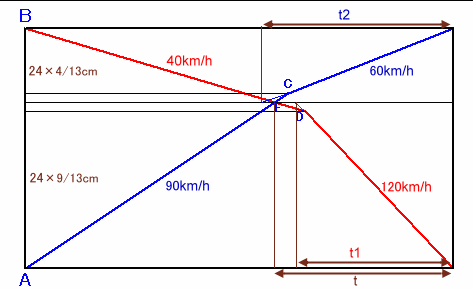
なお、A、D、E、C、Bの順になっているとした場合は、
AE:EB=90:40=9:4なので、
AE=24×9/13、EB=24×4/13kmとなります。EAをトモエさんが120km/sで進んだとしたら、
所要時間t1=24×9/13km/120km/h×60分/h=108/13分。EBをマサルさんが60km/sで進んだとしたら、
所要時間t2=24×4/13km/60km/h×60分/h=96/13分。ダイアグラムから、t1<t<t2でなければならないが、
t1=108/13分>t2=96/13分
なので、不適。