第２３９問の解答

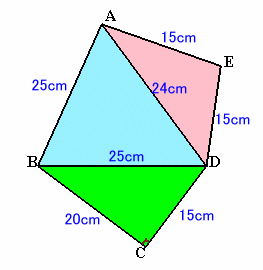
１．問題　［空間図形］

問題図
左図は、ある容器の展開図で、点線部分を折って組み立てます。

では、この展開図を組み立てるとき、その容積は何cm3でしょうか。


ただし、
  • ＡＢ＝ＢＤ＝２５cm、ＡＤ＝２４cm、
  • ＡＥ＝ＥＤ＝ＤＣ＝１５cm、ＢＣ＝２０cm、
  • ＢＣＤ＝９０度

となっています。 

　

２．解答例１（長野美光さん、高田修成さん、Michaelさん、C-Dさん、高橋道広さん、ちーくん、糸瀬善人さん、ゆんななこさん、中村明海さん、M.Hossieさん、q(o_n)pさん、他多数）

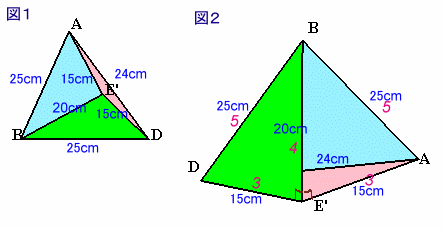
点ＣとＥが重なってできる頂点をＥ'とします。
図１は、△ＡＢＤを底面として真上から、図２は△ＡＤＥ'を底面として斜めから見たところです。

参考図1
（参考）マウスでドラッグして下さい。
Sキーを押すとステレオ画像になります。

△ＢＥ'Ｄと△ＢＥ'Ａは、いずれも３辺が１５、２０、２５ｃｍであり、辺の長さが３：４：５の直角三角形となります。

従って、ＢＥ'はＤＥ'およびＡＥ'に垂直となるので、平面ＡＤＥ'に垂直。
よって、三角錐ＢＡＤＥ'の高さはＢＥ'＝２０ｃｍとなります。

参考図2

△ＡＤＥを２等分すると、斜辺が１５ｃｍ、１辺が１２ｃｍとなるので、辺の長さが３：４：５の直角三角形となるので、もう１辺の長さ、 すなわち△ＡＤＥの高さは９ｃｍとなります。

よって、求める容積＝三角錐ＢＡＤＥ'＝1/3×（1/2×２４×９）×２０＝７２０ｃｍ3となります。

　答：７２０cm3

　

以上