第２４０問の解答

１．問題　［整数の性質］

　各位の数を足し算すると１３の倍数になるような数を考え、小さいほうから順に並べてみます。

　　　　４９、５８、６７、７６、８５、９４、１３９、・・・・・

　このとき、となり同士の数字の間隔は、最も大きいところでいくつになっているでしょうか。
その“間隔”を答えてください。

２．解答例１（中村明海さん、Michaelさん、Taroさん、Gouさん、たこやき大学さん、ちえんかん＃２期さん、あんみつさん、C-Dさん、うっしーさん、トトロ＠Ｎさん、高橋道広さん、M.Hossieさん、有無相生さん、ちーくん、他多数）

今回は、中村明海さんの証明が詳しいので、これをご紹介することにします。

整数を百位以上の「上位桁」とそれ未満の「下位桁」に分けて考えます。

（１）与えられた「上位桁」に対する「下位桁」の配列

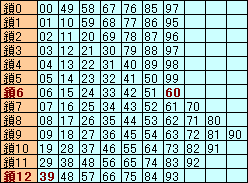
００～９９までの１００個の整数を１３で割った余りがｍであるものを小さい順につないだものを（鎖ｍ）と名づけます。
例えば、「上位桁」が１２３だとすると、その桁の和は６。

従って、下位桁の和は、１３－６＝７。つまり下記（鎖７）の０７～７０が「下位桁」につくことになります。

（２）鎖の中での最大間隔

　これは（１）を眺めてわかるように４９です。これがひとつの候補。

（３）鎖のつなぎ目の最大間隔

鎖の終端が最小となるのは、（鎖６）のときで６０。
鎖の先端が最大となるのは、（鎖１２）のときで３９。

もし、（鎖６）から（鎖１２）に繋がることがあれば、それが最大で、間隔は３９－６０＋１００＝７９になります。

では、（鎖６）から（鎖１２）につながるための条件を調べてみましょう。
　　□９９・・９６０→△００・・０３９（ただし△＝□＋１）
（鎖６）の上位桁の和を１３で割った余り（以下、単に余りといいます）は１３－６＝７、
（鎖１２）の上位桁の和の余りは１３－１２＝１。

△＝１のとき、余りは１ですから、□＝０として、９９・・９（ｎ桁）という数で余りが７となるものを見つけるてみましょう。
すなわち、９ｎの余りが７となればいいわけです。
９と１３は互いに素ですから、このようなｎは必ず存在します。

つまり、ｎ＝８のときが、条件を満たす最小値です。

（４）結論