第２４３問の解答

１．問題　［整数の性質］

  • 大きさの同じ立方体がたくさんあります。これらの立方体を積み上げて、直方体を作りました。
    まず、この直方体の１つの面をペンキで塗りました。
  • 次に、残った５面の中から互いに向かい合わない２面を選んでペンキを塗りました。
    すると、ペンキが塗られていない立方体が６０３個だけ減ったそうです。
  • さらに、残った３面の中から互いに向かい合った２面を選んでペンキを塗りました。
    すると今度は、ペンキが塗られていない立方体が１３０個減ったそうです。

（１）ペンキの塗られていない立方体は何個になったでしょうか。
（２）もとの直方体は立方体を何個使って作られていたでしょうか。
　　　考えられる数のうち、最も大きいものを答えてください。

２．解答例１（高橋道広さん、M.Hossieさん、DrKさん、他多数）

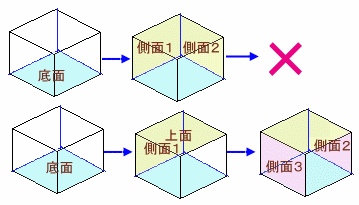
まずペンキを塗る順番を考えます。

参考図1

最初に底面を塗るものとします。
次に、側面から隣り合う面を２個を選んで塗ると、最後に塗るべき向かい合う面がなくなってしまうので不適です。
よって、２番目には上面と側面１個を塗り、最後に側面から向かい合う２面を塗ることになります。

参考図2

立方体の１辺の長さを１、直方体の各辺の長さをｘ、ｙ、ｚとします。

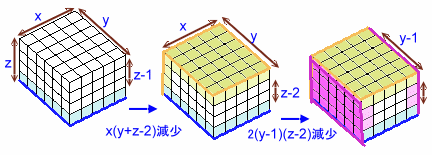
　・最初：立方体の個数　・・・　ｘｙｚ個
　　　　↓　-xy
　・底面を塗った後　・・・　xy(z-1)個
　　　　↓　-x(y+z-2)
　・底面と側面を塗った後　・・・　x(y-1)(z-2)個
　　　　↓　-2(y-1)(z-2)
　・向かい合う側面を塗った後　・・・　(x-2)(y-1)(z-2)個

従って、
　　x(y+z-2)＝６０３　・・・　（１）
　　2(y-1)(z-2)＝１３０　・・・（２）

（２）より、(y-1)(z-2)＝６５
　６５＝１×６５＝５×１３と分解されるので、
　(y-1、z-2)＝(1、６５)、(６５、１)、(５、１３)、(１３、５)すなわち、
　(y、z)＝(２、６７)、(６６、３)、(６、１５)、(１４、７)
となります。
　６０３＝９×６７と分解されるので、（１）より、
はじめの２つのケースではy+z-2=６７となり、ｘ＝９、
後の２ケースではy+z-2=１９となり、ｘは整数でないので不適。

従って、設問１の答は、
　　(x-2)(y-1)(z-2)＝７×６５＝４５５個
と分かります。

設問２については、
　　(y、z)＝(２、６７)のとき、ｘｙｚ＝１２０６
　　(y、z)＝(６６、３)のとき、ｘｙｚ＝１７８２
となり、後者のほうが大きいので答は１７８２個となります。


　答：（１）４５５個（２）１７８２個

以上