第２４４問の解答

１．問題　［場合の数］

ある人数の子ども達が横一列に並びます。　この列を眺めたとき、
  • 「男の子の右どなりに女の子がいる」ような部分が３ヶ所
  • 「女の子の右どなりに男の子がいる」ような部分が２ヶ所
  • 「男の子のとなりに男の子がいる」ような部分が４ヶ所
  • 「女の子のとなりに女の子がいる」ような部分が３ヶ所できていました。

　では、このような子ども達の並び方は何通りあるでしょうか。

２．解答例１（ミミズクはくず耳さん、たなかさん、小杉原啓さん、高橋道広さん、克直さん、mhayashiさん、トトロ＠Ｎさん、M.Hossieさん、他多数）

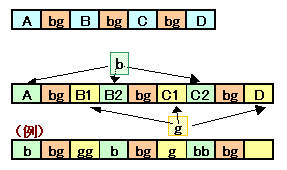
男の子をb、女の子をgと表すことにすると、bgと並ぶものが必ず３カ所あります。

参考図1

上記B、Cの部分の並びがどうあろうとも、必ずgbの配置が少なくとも２カ所あることが分かります。

もし、Ａの部分にgが入るとgbと並ぶものが増えるので、Ａの部分にはbのみしか配置できません。
同じく、Ｄの部分にbが入るとgbと並ぶものが増えるので、Ｄの部分にはgのみしか配置できません。

同様に、Ｂ、Ｃの部分には、前半部分（Ｂ１、Ｃ１）はgが、後半部分（Ｂ２、Ｃ２）はbが並ぶことになります（０個を含む）。

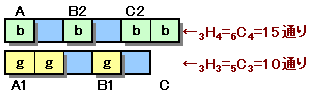
そして、bbと並ぶのが４カ所なので、Ａ、Ｂ１、Ｃ１へｂが０以上入り、合計４個となります。これはちょうど、Ａ、Ｂ１、Ｃ１という３種類のものから重複を許し４個選ぶのと同じことになるので、3Ｈ4＝3+4-1Ｃ4＝１５通りあります。

同様に、ggと並ぶのが３カ所なので、Ｂ２、Ｃ２、Dへgが０以上入り、合計３個となります。これはちょうど、Ｂ２、Ｃ２、Dという異なるものから重複を許し３個選ぶのと同じことになるので、3Ｈ3＝3+3-1Ｃ3＝１０通りあります。（下図参照）

参考図2

そして、これらの選び方はお互いに影響を受けない（独立事象）ので、求める場合の数は、合計１５×１０＝１５０通りとなります。

　答：１５０通り

以上

３．解答例２（あんみつさん、有無相生さん、数楽者さん、きょえぴさん、中村明海さん、圭太さん、BossFさん、ゆんななこさん、他多数）

男の子(b)が７人、女の子(g)が６人でいちばん左が男なのは容易に分かります。
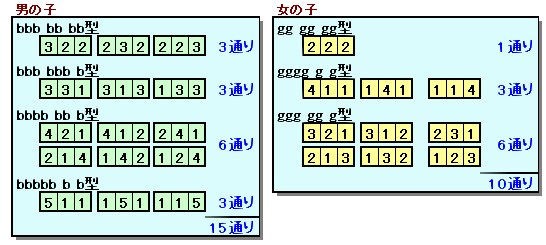
性別が同じ人の固まりを考えると、男の子も女の子も、それぞれ３個ずつの固まりができることになります。

参考図3

参考図4

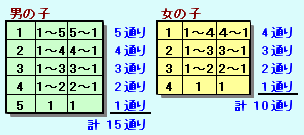
上図から、男の子の並び方は１５通り、女の子の並び方は１０通りあることが分かります。

そして、男の子と女の子の組み合わせ方は、下図のように互い違いになりますので、
結局求める場合の数は、１５×１０＝１５０通りになります。

参考図5


なお、上記３つの固まりの場合の数は、解答例１と同様に重複組み合わせで求めることもできます。

それぞれの固まりには必ず１人以上いますから、これらを除いて考えると、
男の子は７−３＝４人を３つの固まりに配置することになるので、
　　3Ｈ4＝3+4-1Ｃ4＝１５通り、
女の子は６−３＝３人を３つの固まりに配置することになるので、
　　3Ｈ3＝3+3-1Ｃ3＝１０通りと求まります。