第２４５問の解答

---

１．問題　［平面図形］

左図のような、ＡＤ＝３cm、ＢＣ＝７cmの台形ＡＢＣＤがあります。 この台形ＡＢＣＤの辺ＡＢの中点Ｍと頂点Ｄを結んだところ、 ＭＤ＝６cm、∠ＡＤＭ＝∠ＣＤＭとなりました。 では、この台形ＡＢＣＤの面積は何cm2でしょうか。

---

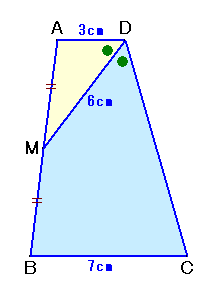２．解答例１（C-Dさん、ミミズクはくず耳さん、noetherさん、高橋道広さん、圭太さん、萬田銀次郎さん、糸瀬善人さん、中村亮さん、他多数）

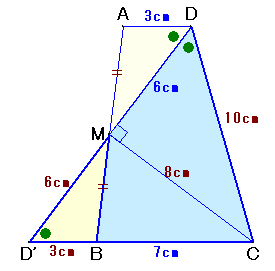
DMとBCをそれぞれ延長し、交点をD'とします。

△ＡＭＤと△ＢＭＤ'について、
　∠ＡＭＤ＝∠ＢＭＤ'、∠ＡＤＭ＝∠ＢＤ'Ｍ（錯角）およびＡＭ＝ＢＭより、
△ＡＭＤ≡△ＢＭＤ'。
よって、Ｄ'Ｍ＝ＤＭ＝６ｃｍ、Ｄ'Ｂ＝ＡＤ＝３ｃｍ。

∠ＣＤＭ＝∠ＣＤ'Ｍより△ＣＤＤ'は二等辺三角形、
よってＣＤ＝ＣＤ'＝１０ｃｍ。

従って、△ＣＤＭおよび△ＣＤ'Ｍは、辺の長さが３：４：５の直角三角形となり、ＣＭ＝８ｃｍと分かります。

よって、△ＡＭＤ＝△ＢＭＤ'だから、
台形ＡＢＣＤ＝△ＣＤＤ'＝1/2×１２×８＝４８ｃｍ²。

答：４８cm²

以上

---

３．解答例２（Taroさん、小杉原啓さん、うっしーさん、ちーくん、うりょさん、ちえんかん＃２期さん、他多数）

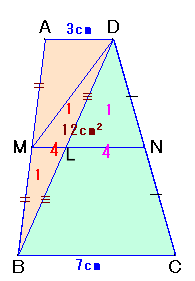
ＭからＢＣと平行に直線を引き、ＣＤとの交点をＮ、
ＮからＭＤに下ろした垂線の足をＥ、ＤＢとＭＮの交点をＬとします。

　　

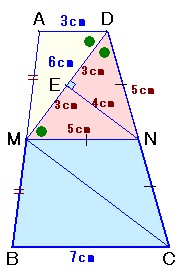
中点連結定理より、
　ＭＬ＝ＡＤ×1/2＝１．５ｃｍ、ＬＮ＝ＢＣ×1/2＝３．５ｃｍ、
よって、ＭＮ＝ＭＫ＋ＬＮ＝１．５＋３．５＝５ｃｍ。

∠ＭＤＮ＝∠ＤＭＮ（錯角）より、△ＮＤＭは二等辺三角形、
よって、ＤＮ＝ＭＮ＝５ｃｍ。

また、ＥはＤＭの中点となるので、ＤＥ＝ＥＭ＝３ｃｍ、
よって、△ＮＤＥおよび△ＮＭＥは辺の長さが３：４：５の直角三角形となります。
従って、△ＮＤＭ＝1/2×６×４＝１２ｃｍ²。

△ＤＬＮ∽△ＤＢＣで相似比は１：２、よって△ＤＬＮ：△ＤＢＣ＝１：４。・・・（１）

△ＤＭＬと△ＢＭＬは底辺が共通で高さが等しいので△ＤＭＬ＝△ＢＭＬ。
また、△ＢＭＬ∽△ＢＡＤで相似比は１：２、よって△ＢＭＬ：△ＢＡＤ＝１：４。
従って、△ＤＭＬ：△ＢＡＤ＝１：４。・・・（２）

（１）、（２）より、
台形ＡＢＣＤ＝△ＢＡＤ＋△ＤＢＣ＝△ＤＭＬ×４＋△ＤＬＮ×４
　＝△ＤＭＮ×４＝１２×４＝４８ｃｍ²。

---