第246問の解答
1.問題 [場合の数]
|
1〜14までの数の書かれたボールが1個ずつ、全部で14個あります。 いま、あるクラスの出席番号1番〜12番までの生徒12人がボールを1人1個ずつ取ります。 このとき、12人全員が、「自分の出席番号よりもボールに書かれた数のほうが大きい」ような場合は何通りあるでしょうか。 |
2.解答例1(C-Dさん、糸瀬善人さん、高橋道広さん、地蔵さん、有無相生さん、M.Hossieさん、ゆんななこさん、他多数)
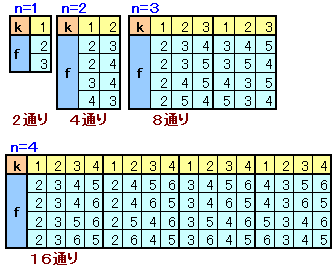
人数がn=1〜4までを数えてみると下図のようになります。
場合の数は、fn=2nと予想されます。
1番の人から考えていくと、例えばn=4のとき、1番の人が5のボール、2番の人が6のボールをとってしまうと4番の人が取るボールがなくなってしまいますので単純にはいきません。
そこで、逆に最後の人から考えていくことにします。
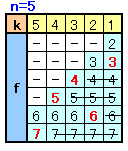
例えば、n=5のとき、
5番の人が取ることができるボールは6〜7の2通り、
4番の人は5〜7の3通りから5番の人が取ったものを除く2通り
3番の人は4〜7の4通りから5番、4番の人が取ったものを除く2通り
2番の人は3〜7の5通りから5〜3番の人が取ったものを除く2通り
1番の人は2〜7の6通りから5〜2番の人が取ったものを除く2通り
となるので、結局25=16通りとなります。同様にして、n=12のときは、212=4096通りとなります。
答:4096通り
以上
3.解答例2(DrKさん、小西孝一さん、うっしーさん、ちーくん、うりょさん、ちえんかん#2期さん、他多数)
n人のときの場合の数fnに関して、漸化式を考えることにしましょう。
しかしながら、各人が取ることのできるボールの番号は、nが増えるにつれて増加しますので、結構面倒です。
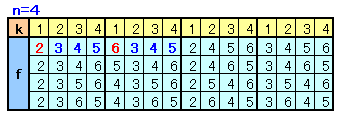
そこで、n-1人のとき、1〜n-1番目の人が取ったボールの番号をa1、a2、・・・、an-1とします。
これに対して、各人の番号と取ったボールの番号の両方を、それぞれ1加えた場合を対応させることにします。
(すなわち、a2=a1+1、a3=a2+1、・・・、an=an-1+1)a2、a3、・・・、anは、3〜n+2のn個の数からn-1個選んだことになるので、あと1個残っているものがあります。1番の人が取ることができるのは、2とその番号の2通りになります。
以上のことから、fn=2fn-1と求まりますので、
fn=2fn-1=22fn-2=23fn-3・・・=2n-1f1=2n
となります。従って、本問ではf12=212=4096通りです。