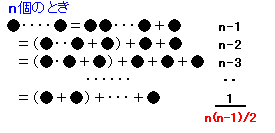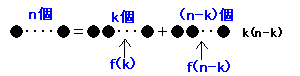第２４７問の解答

１．問題　［規則性］

何個かの碁石が山になっています。
まず、この山を２つに分けます。分けた山をさらに２つに分け・・・という作業を全部の山が１個ずつになるまで続けます。
また、山を２つに分けるたびに、２つの山の碁石の数をかけた数をノートに記録します。

すると、ノートに記録された数の合計は１２０であったそうです。
では、碁石は何個あったでしょうか。

２．解答例１（Taroさん、たなかさん、丸天後藤様、むらかみさん、中村明海さん、あんみつさん、ＫＩＮさん、ＴＯＲＡさん、名倉っちさん、ふじさきたつみさん、BossFさん、M.Hossieさん、有無相生さん、鈴木オヤジさん、うっしーさん、他多数）

山の分け方によらないと仮定して、１個ずつ分けていくことにします。

参考図1 参考図2

碁石の数がｎ個とします。
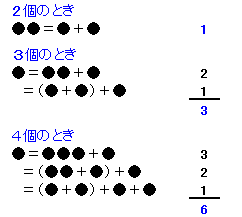
最初の１個を分けると、記録する数は１×（ｎ−１）＝ｎ−１
２番目の１個を分けると、記録する数は１×（ｎ−２）＝ｎ−２
３番目の１個を分けると、記録する数は１×（ｎ−３）＝ｎ−３
　・・・
となり、記録した数の合計は、
　１＋２＋・・・＋（ｎ−１）＝ｎ（ｎ−１）／２
となります。

参考図3

ｎ（ｎ−１）／２＝１２０より、ｎ＝１６個と分かります。


碁石の数がn個のとき、記録した数の合計をf(n)とします。
山の分け方によらず、f(n)＝n(n-1)/2・・（A）となることを帰納法で示します。

（１）n＝2のとき、f(2)＝2・1/2＝２となり、OK.

（２）（n-1）個以下のとき、（A）が成り立つと仮定。

　　ｎ個のとき、まずk個と（n-k）個に分けたとすると、

参考図4

　f(n)＝f(k)＋f(n-k)＋k(n-k)　・・・（B)
　　　＝k(k-1)/2＋(n-k)(n-k-1)/2＋k(n-k)
　　　＝k(k-1)/2＋{n2/2−(2k+1)/2・n＋k(k+1)/2}＋kn-k2
　　　＝n2/2−n/2
　　　＝n(n-1)/2

よって、n個のときも（A)は、成り立つ。

以上から、数学的帰納法により、（A)は任意のｎ（ｎ≧2）で成り立つことが分かる。

答：１６個

以上

３．解答例２（ヒデー王子さん、数楽者さん、他）

同じ山にある碁石は互いにひもで結ばれていると考えることにしましょう。
碁石がn個あれば、ひもの数はnC2＝n(n-1)/2本。

参考図5　　

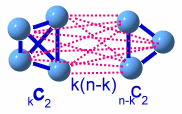
n個ある碁石をk個と(n-k)個に分けたとき、
k個の山の碁石は、ひもの数kC2＝k(k-1)/2本、
(n-k)個の山の碁石は、ひもの数n-kC2＝(n-k)(n-k-1)/2本、
そして２つに分かれた碁石間のひもk(n-k)本は切ることになる。
（これは、解答例１の（B)に対応している）

すなわち、本問題の２つに分けたときに記録する数は、この切ったひもの本数に等しい。

従って、全部の山の碁石がすべて１個になったときは、全てのひもを切ったことになるので、記録された数の合計は元のひもの本数n(n-1)/2本に等しい。

以下、解答例１と同様。

（その他の解法）