第２４８問の解答

１．問題　［場合の数］

問題図

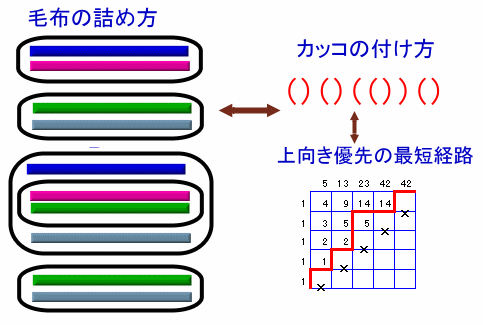
上図は、折りたたんで積まれた４枚の毛布を２枚の袋をつかって袋詰めしたところを表しています。袋詰めするときには、
  1. 毛布の順番は入れ換えない。
  2. それぞれの袋の中には偶数枚（２枚以上）の毛布が入っているようにする。
  3. １つの毛布が２枚以上の袋に包まれていても良いが、その場合は、２枚の袋の内側の面と外側の面が（側面以外で）接してはならない。

という３つのルールを守ることになっています。
すると、毛布が４枚の場合には、上図のように、Ａ・Ｂの２パターンの袋詰めの方法があることが分かります。

では、毛布が１０枚、袋が５枚あったとすると、袋詰めの方法は何通りあるでしょうか。

２．解答例１（noetherさん、ヒデー王子さん、あんみつさん、数楽者さん、馬渕の算数星人さん、ＫＩＮさん、他）

カタラン数の問題に帰着できることを示します。

各袋のすぐ内側には、その中に袋があれば上下１枚ずつ合計２枚以上の毛布が存在します。また、一番内側の袋にも偶数枚、すなわち２枚以上の毛布があります。

ところが、毛布の枚数１０は、袋の枚数５の２倍なので、結局各袋の内側にはちょうど２枚ずつ毛布があることが分かります。

従って、袋の状態が決まれば毛布の詰め方は一意的に決まることになるので、袋の関係さえ考えればいいことになります。

参考図1

袋の上側を左カッコ、下側を右カッコとすればカッコの付け方と対応し、
また左カッコを格子路の上向き、右カッコを右向きと対応させれば、
上向き優先の最短経路と対応します。

これは、いわゆるカタラン数になりますので、Ｋ5＝10Ｃ5/6＝４２通りとなります。（上図では、最短経路数を数え上げています。）

答：４２通り

以上

（その他の解法）