第２４９問の解答

１．問題　［空間図形］

問題図

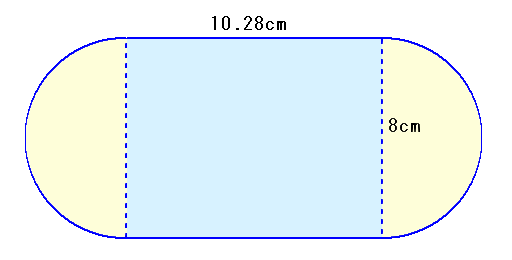
上の図は、直径８cmの半円２つと、タテ８cm、ヨコ１０.２８cmの長方形が組み合わされた形をしたブリキの板を表しています。

この板をカッターで切断して２つの部品に分け、それらを組み合わせて立体を作ります。

　このとき、完成した立体の体積は何cm3でしょうか。ただし、円周率が必要な場合は３.１４として計算してください。

　ただし、切断によってできる線は直線１本で、２つの部品はともに１本だけ折り目の線がつくものとします。また、完成した立体は“穴の空いていない”立体となります。

２．解答例１（Taroさん、Mikiさん、たなかさん、むらかみさん、トトロ＠Ｎさん、CRYING DOLPHINさん、ゆんななこさん、noetherさん、高橋道広さん、ミミズクはくず耳さん、あんみつさん、いなさん、Hossieさん、sodoさん、名倉っちさん、小西孝一さん、他多数）


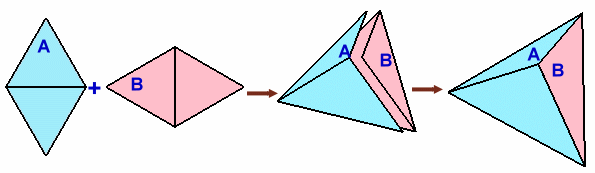
折り目が１本だけ、２個の部品で立体を作る例は図１の四面体、
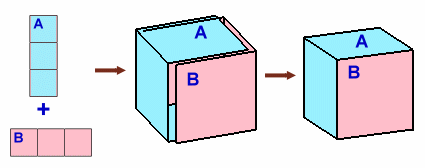
折り目が２本、２個の部品で立体を作るなら図２の六面体があります。 

図１
参考図1
図２
参考図2		 図３
参考図3

本問題では、部品の中に円周部分があるので、図１、図２をベースに、図３のような硬球のボールの例をヒントにして考えてみます。

図４
参考図4
図５
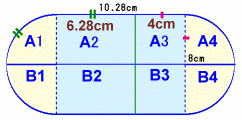
参考図5

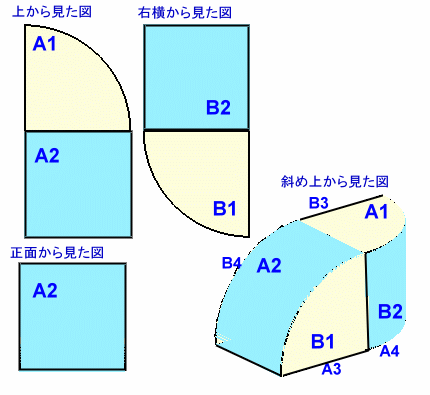
図４のように、板を真横に切断し上下に２分割します。
４分の１円をＡ１、Ａ４とＢ１、Ｂ４とし、また長方形を６．２８ｃｍと４ｃｍで分け、
Ａ２、Ａ３とＢ２、Ｂ３とします。

Ａ３、Ａ４を下辺におき、Ａ３とＡ２のところで折り目を入れます。
Ａ２を半径４ｃｍの円周に沿って曲げていくと、ちょうどＡ１はＡ４の真上にきます。・・・「コ」の字に似た形

同様に、Ｂのほうも同様にＢ３とＢ２のところで折り目、Ｂ２を円周に沿って曲げます。

これらを、組み合わせると図５のようになります。

この立体は、半径４ｃｍ、高さ４ｃｍの円柱の４分の１を２つ、９０度捻って合わせた形となりますので、体積は円柱の半分に等しくなります。

体積＝３．１４×４2×４／２＝１００．４８ｃｍ3

答：１００．４８cm3

以上