第２５０問の解答

---

１．問題　［場合の数］

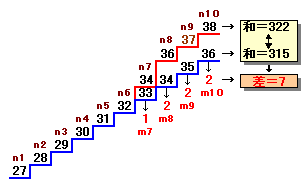
１０個の異なる整数があり、その和は３２２になっています。 いま、この１０個の整数の中で最も小さい数をn1とします。 n1が最も大きくなるようにするとき、１０個の整数の組は何通り考えられるでしょうか。

---

２．解答例１（AUさん、高田修成さん、小杉原啓さん、Mikiさん、Taroさん、ミミズクはくず耳さん、あんみつさん、ＴＯＲＡさん、トトロ＠Ｎさん、中村明海さん、BossFさん、他多数）

１０個の整数をn₁、n₂、n₃、・・・、n₁₀（ただし、n₁<n₂<n₃<・・・<n₁₀）とします。

　　n₂≧n₁+1
　　n₃≧n₂+1≧（n₁+1）+1≧n₁+2
　　n₄≧n₃+1≧（n₂+2）+1≧n₁+3
　　　・・・
　　n₁₀≧n₉+1≧（n₁+8）+1≧n₁+9
一般式としては、n_i≧n₁+(i-1)（ただし、1≦i≦10）が成り立ちます。

ここで、n_i=n₁+(i-1)+m_iとおくと、上記より、m_i≧0。
また、n_i+1-n_i＝{n₁+i+m_i+1}-{n₁+(i-1)+m_i}＝m_i+1-m_i＋１が成り立ち、
　n_i+1-n_i≧1より、m_i+1-m_i≧0（ただし、1≦i≦9）

さて、題意より、
　Σ(i=1..10）n_i
＝Σ(i=1..10）{n₁+(i-1)+m_i}
＝10n₁+Σ(i=1..10）{i-1}+Σ(i=1..10）{m_i}
＝10n₁+45+Σ(i=1..10）{m_i}

よって、
　322＝10n₁+45+Σ(i=1..10）{m_i}
　10n₁＝277-Σ(i=1..10）{m_i}≦277
従って、n₁≦27．7となり、n₁の最大値は、２７と分かります。

よって、Σ(i=1..10）{m_i}＝322-(27×10+45)=7となります。・・・（１）

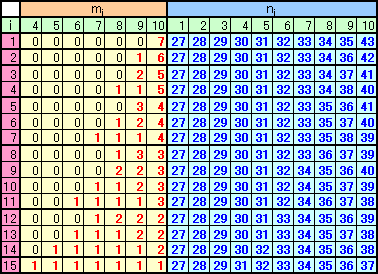
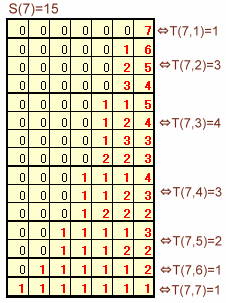
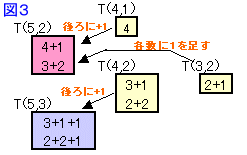
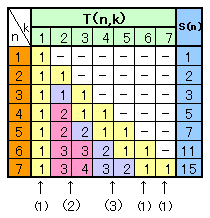
（１）は、求める整数の組が、７を整数の和に分割する場合の数（分割数）に該当することを表しています。

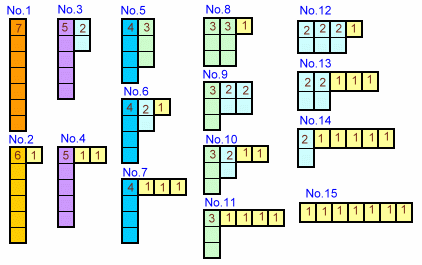
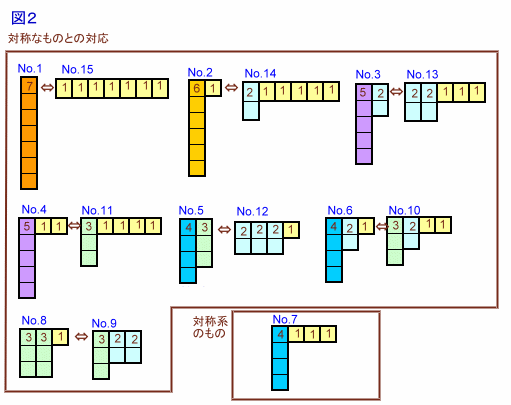
そこで、m₁₀＝７、６、・・・、１のときと順に数え上げれば、下表のとおりとなり、合計１５通りと分かります。

なお、図１は分割後の整数をタイルの数で表したもので、Youngの図（またはFerres図形）と呼ばれています。

また、Youngの図では、図２でNo.1⇔No.15、No.2⇔No.14のように、-45度の直線を対称軸として折り返したものとの対応を考えることができます。

答：１５通り

以上

---

その他の解答例

・n1の最大値が２７であることに着目して数え上げ　・・・
　圭太さん、ちえんかん＃２期さん、ゆんななこさん、mhayashiさん、DrKさん、Hossieさん、他多数

---

（参考）帰納法的に数え上げる方法

整数nの分割数をS(n)、整数nをk個の整数に分割する場合の数をT(n、k)とすると、
　S(n)＝Σ(k=1..n)T(n、k)
と表すことができます。

従って、T(n、k)を求めれば、S(n)を数えることができます。

次式は、容易に分かります。
　T(n、1)＝1、T(n、n-1)＝1、T(n、n)＝1 ・・・　（１）

また、図３より、次式が成り立つことが分かります。
　k＞n/2のとき：T(n、k)=T(n-1、k-1)　・・・　（２）
　k≦n/2のとき：T(n、k)=T(n-1、k-1)+T(n-k、k)　・・・　（３）

（１）、（２）、（３）を用いて、次々とT(n、k)を下表のように求めることができます。

---