第251問の解答
1.問題 [その他(つるかめ算)]
|
マサルさんとトモエさんが、ある大きな水槽に水を入れる作業をしています。 2人は手動ポンプを使って作業しているので、一定間隔ごとに「作業」と「休み」を繰り返しています。また、作業をしているときは、マサルさんは1分間に4リットル、トモエさんは1分間に3リットルの水を水槽に入れることができます。 結局2人は30分で水槽に102リットルの水を入れることができました。この30分間のうち、2人がともに「作業」していた時間の総和と、2人がともに「休み」であった時間の総和は同じで、これらは2人のうち少なくとも一方が「作業」していた時間の総和のちょうど半分であったそうです。 このとき、 (1)「マサルさんだけが作業していた時間の総和」 (2)「トモエさんだけが作業していた時間の総和」 をそれぞれ求めてください。 |
2.解答例1(ちえんかん#2期さん、Gouさん、高橋道広さん、ゆんななこさん、M.Hossieさん、トトロ@Nさん、長野美光さん、他多数)
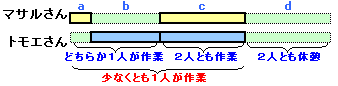
下図のように線分図で考えます。
題意より、「どちらかが作業している時間の総和」、「2人とも作業している時間の総和」および「2人とも休憩している時間の総和」は全て等しくなるので、それぞれ10分と分かります。
(式)
(a+b+c)/2=c=d
(a+b)+c+d=30 より、a+b=c=d=10を得る。「2人とも作業している時間」では、1分あたり4+3=7リットル入れられるので、合計10分間で7×10=70リットル入れられます。
従って、「どちらか1人が作業している」10分間では、102−70=32リットル入れたことになります。
もし仮に、この10分間、トモエさんだけが作業していたとすると、3×10=30リットルしか入れられません。
トモエさんの替わりにマサルさんが作業すると1分あたり4−3=1リットルよけいに水を入れることができますので、32−30=2リットル多く入れるには2分間マサルさんが作業したことになります。
従って、トモエさんは10−2=8分間作業したことになります。
(式)
a+b=10 ・・・ (1)
4a+3b=32 ・・・ (2)
(2)−(1)×3よりa=2、(1)×4−(2)よりb=8を得ます。
答:(1)2分 (2)8分
以上
3.解答例2(小杉原啓さん、うっしーさん、他)
「2人とも作業している時間の総和」と「2人とも休憩してる時間の総和」は等しいので、下図のように時間を入れ替えて考えます。
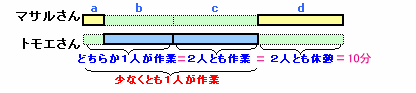
マサルさんの作業時間計をX=a+c=a+d、
トモエさんの作業時間計をY=b+c とおくと、
X+Y=30
4X+3Y=102 より、X=12、Y=18を得る。単独で作業している時間は、
マサルさん:X−d=12−10=2分、
トモエさん:Y−c=18−10=8分 となります。